티스토리 뷰
티스토리 렌더링 문제로 수식이 많이 깨진다. 일단 깨진 형태로 올려두지만 쉽게 볼 수 있는 PDF를 첨부한다. PDF를 보는 것을 추천한다.
이번 글에서는 다음과 같은 쿼리를 수행하는 자료 구조에 대해 다룬다:
- 길이 $N$ 의 수열 $A$ 와 $Q$ 개의 쿼리 $1 \le i \le j \le N$ 가 주어질 때, $A[i], A[i + 1], \ldots, A[j]$ 의 최장 증가 부분 수열 (Longest Increasing Subsequence, LIS) 를 계산하라.
LIS 문제의 경우 동적 계획법으로 해결할 수 있는 가장 기초적인 문제 중 하나로, 수학적으로 여러 의미를 가지기 때문에 변형된 문제들이 다방면으로 연구되고 있다. 위와 같은 쿼리 문제는 다들 자료 구조 문제를 고민해 보다가 한번쯤 생각해 봤을 정도로 기초적인 문제 종류 중 하나이다. 본인은 오랜 시간 동안 위와 같은 쿼리를 풀 수 없다고 생각하다가 최근에 이를 $O(N \log^2 N + Q \log N)$ 시간에 해결하는 semi-local string comparison 이라는 논문을 발견하게 되었다. 그 내용 자체가 상당히 흥미롭고, LIS 문제 외에도 고민해 볼 거리가 많은 것 같아서 이를 이번 소프트웨어 멤버쉽 글로 소개하게 되었다. 한국 뿐만 아니라 외국 사람들도 잘 모르는 기술일 것 같아서, Codeforces에도 동일한 글을 영어로 작성하였다.
semi-local string comparison 을 소개하는 원 논문은 굉장히 길며 복잡한 수학적 용어들을 많이 사용한다. 이를 qwerasdfzxcl 이 짧게 정리했지만, 원리와 이해에 대해서는 설명을 생략한 자료이다. 오랜 기간 연구한 끝에 이러한 복잡한 수학 지식 없이 나름대로 간단하게 이 테크닉을 이해하는 방법을 찾았다. 여전히 아주 간단하지는 않지만, 이번 글을 통해서 많은 사람들이 더 고민해 보고 더욱 더 간단한 해석을 찾으면 그것도 의미가 클 것 같다.
Chapter 1. The All-Pair LCS Algorithm
위 문제의 일반화된 버전을 생각해보자:
- 길이 $N$ 의 수열 $S$, 길이 $M$ 의 수열 $T$, $Q$ 개의 쿼리 $1 \le i \le j \le M$ 이 주어질 때, $S$ 와 $T[i], T[i + 1], \ldots, T[j]$ 의 최장 공통 부분수열 (LCS, Longest Common Subsequence) 를 계산하라.
위 문제가 구간 LIS 문제의 일반화인 이유는 다음과 같다: $(A[i], -i)$ 를 좌표압축 할 경우 $A$ 를 길이 $N$ 의 순열로 볼 수 있고, 순열 $A$ 의 LIS는 $A$ 와 $[1, 2, \ldots, N]$ 의 LCS와 같기 때문이다. 고로 위 자료구조를 $S = [1, 2, \ldots, N], T = A$ 로 초기화하면 LIS 쿼리를 응답하는 자료구조를 구성할 수 있다.
구간 LCS 문제는 LIS와 유사하게 그 자체로도 흥미로운 문제가 될 수 있다. 예를 들어, Cyclic LCS 역시 구간 LCS를 해결하면 풀 수 있고, 예전 Petrozavodsk 문제 중에서도 구간 LCS에 대한 문제가 있었다. 구간 LCS는 $O(N^2 + Q)$ 시간에 해결할 수 있는 다양한 풀이가 존재하며 ($N = M$ 이라 가정) 예를 들어 본인의 예전 글에 소개된 Andy Nguyen의 Cyclic LCS 풀이 를 응용해서 해결할 수도 있다. 하지만 이들 중 LIS 문제의 $O(N \log^2 N)$ 과 연관이 있는 풀이는 An all-substrings common subsequence algorithm 논문에 나온 풀이 뿐이다.
LCS 문제의 일반적 풀이에 사용되는 DP 테이블을 생각하자. 상태 및 상태 전이는 그리드 형태의 Directed Acyclic Graph (DAG) 라고 생각할 수 있다. 정확하게는, 다음과 같은 그래프이다:
- 상태 $(i, j)$ 에 대응되는 $(N+1) \times (M+1)$ 개의 정점
- $(i, j)$ 에서 $(i+1, j)$, $(i, j+1)$ 로 가는 가중치 0의 간선
- $S[i+1] = T[j+1]$일 때 $(i, j)$ 에서 $(i+1, j+1)$ 로 가는 가중치 1의 간선
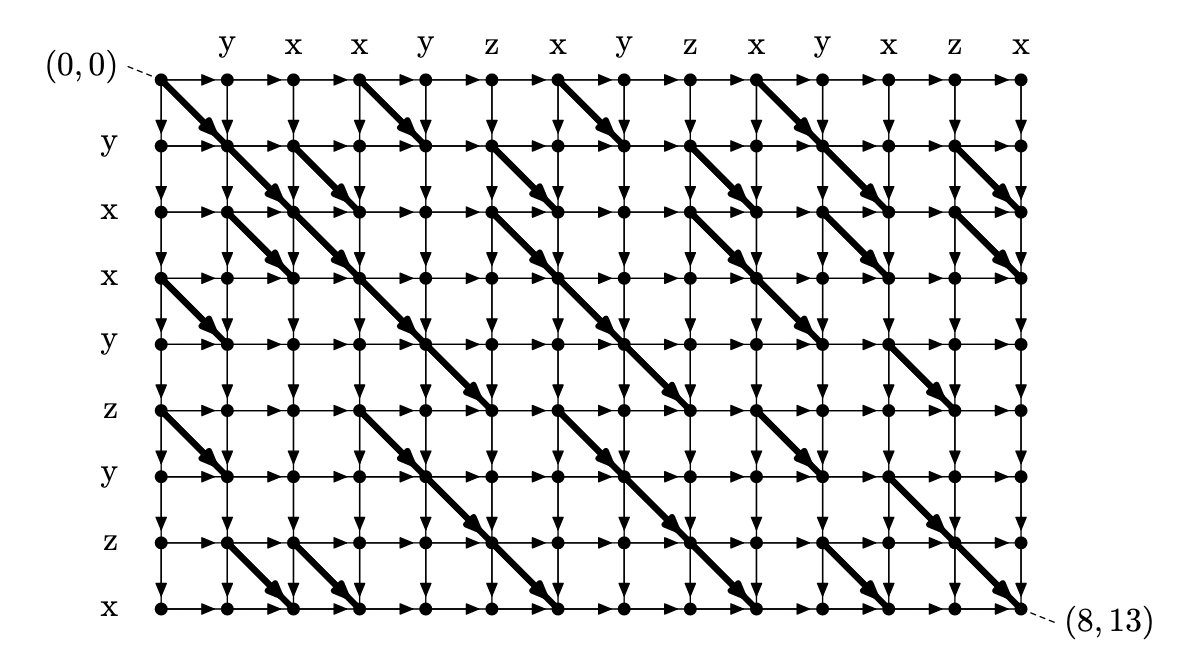
쿼리 $(i, j)$ 에 대한 답은 이 그래프의 정점 $(0, i-1)$ 에서 정점 $(N, j)$으로 가는 최장 경로의 길이와 같다. $(x_1, y_1)$ 에서 $(x_2, y_2)$ 로 가는 최장 경로의 길이를 $dist((x_1, y_1), (x_2, y_2))$ 라 하자. 목표는 $dist((0, i), (N, j))$ 를 모든 $0 \le i < j \le M$ 에 대해 계산하면 된다. 이를 위해서는 몇 가지 Lemma가 필요하다.
Lemma 1. $dist((0, y), (i, j)) - dist((0, y), (i, j-1))$ 는 $0$ 혹은 $1$.
Proof.
- $dist((0, y), (i, j-1)) \le dist((0, y), (i,j))$: 그 외 경우 $(i, j-1)$ 로 가는 경로를 오른쪽 방향 간선으로 확장할 수 있다.
- $dist((0, y), (i, j-1)) \geq dist((0, y), (i, j)) - 1$: 그 외 경우 $(i, j)$ 로 가는 경로를 $j-1$ 번 열에서 자르고 아래로 이동할 수 있다.
$\blacksquare$
Lemma 2. $dist((0, y), (i, j)) - dist((0,y ), (i-1, j))$ 는 $0$ 혹은 $1$.
Proof. Lemma 1과 동일. $\blacksquare$
Lemma 3. 모든 $i, j$에 대해 정수 $0 \le i_h(i, j) \le j$ 가 존재하여
- 모든 $i_h(i, j) \le y < j$ 에 대해 $dist((0, y), (i, j)) - dist((0, y), (i, j-1)) = 1$
- 모든 $0 \le y < i_h(i, j)$ 에 대해 $dist((0, y), (i, j)) - dist((0, y), (i, j-1)) = 0$
Proof. 위 명제는 다음과 동치이다: 모든 $y, i, j$ 에 대해 $dist((0, y), (i, j)) - dist((0, y), (i, j-1)) \le dist((0, y+1), (i, j)) - dist((0, y+1), (i, j-1))$. $(0, y) \rightarrow (i, j)$ 를 잇는 최적 경로와 $(0, y+1) \rightarrow (i, j-1)$ 를 잇는 최적 경로를 생각해 보자. DAG가 평면 그래프이니, 두 경로는 교차한다. 두 경로의 도착점을 교환하면, 같은 비용의 두 경로 $(0, y) \rightarrow (i, j-1)$, $(0, y + 1) \rightarrow (i, j)$를 얻으며 이 경로의 비용 합은 최적 경로의 비용 합 이하이다. 고로 $dist((0, y), (i, j)) + dist((0, y+1), (i, j-1)) \le dist((0, y+1), (i, j)) + dist((0, y), (i, j-1))$ 이 성립한다. $\blacksquare$
Lemma 4. 모든 $i, j$에 대해 정수 $0 \le i_v(i, j) \le j$ 가 존재하여
- 모든 $i_v(i, j) \le y < j$ 에 대해 $dist((0, y), (i, j)) - dist((0, y), (i-1, j)) = 0$.
- 모든 $0 \le y < i_v(i, j)$ 에 대해 $dist((0, y), (i, j)) - dist((0, y), (i-1, j)) = 1$
Proof. Lemma 3과 동일. $\blacksquare$
모든 $i, j$ 에 대해 $i_h(i, j)$ 와 $i_v(i, j)$를 계산했다고 하자. 이를 토대로 $dist((0, i), (N, j))$ 를 계산하려면 어떻게 해야 할까? 식을 정리해 보면:
$dist((0, i), (N, j))$
$= dist((0, i), (N, i)) + \sum_{k = i+1}^{j} dist((0, i), (N, k)) - dist((0, i), (N, k-1))$
$= 0 + \sum_{k = i+1}^{j} (i_h(N, k) <= i)$
결론적으로, 전체 값이 필요한 것도 아니고 $i_h(N, *)$ 만 알면 쿼리를 계산할 수 있다. $i_h(N, *)$ 배열 값이 주어진다고 하면, 쿼리들은 $O(\log N)$ 시간에 Fenwick tree를 사용하거나, $O(1)$ 시간에 2차원 부분합을 사용하여 계산할 수 있다. (2차원 부분합은 초기화에 $O(N^2)$ 시간이 필요.)
고로 $i_h, i_v$ 값을 계산하는 것만이 남았으며, 놀랍게도 이것은 아주 간단한 점화식으로 계산이 가능하다.
Theorem 5. 다음이 성립한다:
- $i_h(0, j) = j$
- $i_v(i, 0) = 0$
- $i, j \geq 1, S[i] = T[j]$ 에 대해
- $i_h(i, j) = i_v(i, j-1)$
- $i_v(i, j) = i_h(i-1, j)$
- $i, j \geq 1, S[i] \neq T[j]$ 에 대해
- $i_h(i, j) = \max(i_h(i-1, j), i_v(i, j-1))$
- $i_v(i, j) = \min(i_h(i-1, j), i_v(i, j-1))$
Proof. Base case는 자명하다. 고정된 $y$에 대해, $(0, y)$ 에서 셀 사각형의 네 꼭지점 $(i-1, j-1), (i-1, j), (i, j-1)$ 으로 가는 거리를 고정하자. $t = dist((0, y), (i-1, j-1))$ 라 하면 이에 인접한 두 꼭짓점의 거리는 $t$ 거나 $t + 1$ 이다. 가능성은:
- $dist((0, y), (i-1, j))$ 의 값이 $t$ 인지 $t + 1$ 인지 ($y \ge i_h(i - 1, j)$ 과 동치)
- $dist((0, y), (i, j-1))$ 의 값이 $t$ 인지 $t + 1$ 인지 ($y < i_v(i, j-1)$ 과 동치)
- $S[i] = T[j]$ 인지 아닌지
이 세 정보가 $dist((0, y), (i, j))$ 을 유일하게 결정하며, $2^3 = 8$ 가지 경우를 모두 따져보면 Theorem 5를 증명할 수 있다. $\blacksquare$
Remark. 원본 논문에 있는 증명이 이러하며 내가 찾은 증명도 이것이다. 아마 노가다가 없는 아주 단순한 설명이 있을 것 같은데, 이에 대해 탐구해 보면 좋을 것 같다.
Theorem 5에 의해 $i_h, i_v$ 를 모두 계산하는 간단한 점화식을 사용할 수 있다. 고로 All-Pair LCS 문제는 $O(NM + Q \log N)$ 시간에 풀 수 있고, 이에 따라 Range LIS 문제 역시 $O(N^2 + Q \log N)$ 시간에 풀 수 있다.
SETH Conjecture 가 참이라는 가정 하에, 두 문자열의 Longest common subsequence는 $O(NM)$ 보다 빠르게 구할 수 없다. 이렇게 보면 현재 알고리즘을 줄이기 어려워 보이지만, LIS의 경우 한 쪽 패턴이 $[1, 2, \ldots, N]$로 고정되어 있다는 사실을 활용하여 시간 복잡도를 줄일 수 있다.
Chapter 2. The Seaweed
DP 과정을 도식화하면 우리가 다루는 구조를 조금 더 깊게 이해할 수 있다. 값 $i_v, i_h$ 를 그리드 그래프의 간선에 연관해서 생각해 보자. 이 경우 매번의 DP 상태 전이는 위/왼쪽 간선에서 값을 골라서, 이를 아래/오른쪽 간선에 매칭시키는 것이라고 볼 수 있다. 그림으로 그리면 다음과 같다:

이 그림에서 초록색 곡선은 값을 나타낸다. 큰 직사각형의 왼쪽 변에서 온 값들은 ("BAABCBCA") $0$이고, 위쪽 변에서 온 값들은 ("BAABCABCABA") $1, 2, \ldots, M$ 이다. 이러한 초록색 곡선을 seaweed (미역) 이라고 부른다. Seaweed를 왼쪽 아래에서 오른쪽 위 방향으로 읽고, 읽은 순서대로 왼쪽 과 오른쪽 으로 상대적 위치를 표현하자. 이러한 관점에서 초기 seaweed들은 증가하는 순으로 정렬되어 있다고 생각할 수 있다.
이제 DP 상태 전이를 다시 살펴보자. $S[i] = T[j]$ 일 경우 두 seaweed가 교차하지 않는다. $S[i] \neq T[j]$ 일 경우 두 seaweed가 교차한다는 것은 왼쪽 seaweed가 오른쪽 seaweed보다 큰 값을 가진다는 뜻이다. 달리 말해, $S[i] \neq T[j]$ 인 셀은 seaweed를 버블 정렬 하는 효과를 준다: 두 인접한 seaweed $i, i + 1$ 이 증가 순으로 나열되어 있으면 ($A[i] < A[i +1]$), 감소 순이 되게 바꿔주는 것이다 ($A[i] > A[i+1]$).
Range LIS에는 이러한 쌍이 $N^2 - N$ 개 존재하니 이 정도 관찰로는 아직 문제를 해결하기 불충분하다. 하지만 이제 최적화를 위한 main idea를 소개할 준비가 되었다.
앞의 조건을 수정해서, 값의 크기와 상관없이 두 인접한 seaweed를 바꾸는 문제를 생각해보자. 우리는 각 연산을 순열 $P$ 로 나타낼 것이다. 이 때 $P(i)$ 는 $i$ 번째 seaweed의 최종 위치를 나타낸다. 만약 우리가 위치 $i_1, i_2, \ldots, i_k$ 에서 인접한 seaweed를 바꾼다고 하자. 기초 순열 $P_i$ 를 다음과 같이 정의하자:
$\begin{equation}P_i(j)=\begin{cases} j+1, & \text{if}\ a=i \newline j-1, & \text{if}\ a=i+1 \newline j, & \text{otherwise}\end{cases} \end{equation}$
이 때 모든 연산의 최종 결과는, $P \circ Q$를 순열의 합성이라고 할 때 ($P \circ Q(i) = Q(P(i))$):
$P = P_{i_1} \circ P_{i_{2}} \circ \ldots \circ P_{i_k}$
로 나타낼 수 있다.
위 결과는 값의 크기와 상관없다 는 조건을 추가해서 문제를 쉽게 만든 것이기 때문에, Range LIS에 그대로 응용할 수는 없다. 여기서 정말 흥미로운 사실이 존재하는데, 조건을 다시 추가했을 때, $\boxdot$ 라는 신기한 연산자가 존재해서:
- $\boxdot$ 는 결합 법칙을 만족한다.
- 전체 연산의 결과가 하나의 순열 $P = P_{i_1} \boxdot P_{i_{2}} \boxdot \ldots \boxdot P_{i_k}$ 로 표현된다.
Chapter 3. The Operator
이 연산자는 정의부터 상당히 어렵고 여러 보조 Lemma를 필요로 한다.
Definition 6. 길이 $N$ 의 순열 $P$ 가 주어졌을 때, $\Sigma(P)$ 는 $(N+1) \times (N+1)$ 의 square matrix로 $\Sigma(P)_{i, j} = |{x|x \geq i, P[x] < j}|$ 이다.
직관적으로 봤을 때 이는 왼쪽 아래 방향의 부분합이다. 예를 들어 $P = [2, 3, 1]$ 라고 하면:
$\Sigma(P) = \begin{bmatrix} 0&1&2&3\newline 0&1&1&2\newline 0&1&1&1\newline 0&0&0&0 \end{bmatrix}$
이는 다음 행렬의 부분합이다: $\begin{bmatrix} 0&0&1&0\newline 0&0&0&1 \newline 0&1&0&0\newline 0&0&0&0 \end{bmatrix}$.
Definition 7. 크기 $N \times M$ 의 행렬 $A$ 와 크기 $M \times K$의 행렬 $B$ 가 주어질 때 min-plus multiplication $A \odot B$ 는 $(A \odot B){i, j} = \min{1 \le k \le M} (A_{i, k} + B_{k, j})$ 로 정의된다.
Theorem 8. 길이 $N$ 의 두 순열 $P, Q$ 가 주어질 때, 길이 $N$ 의 순열 $R$ 이 존재해서 $\Sigma(R) = \Sigma(P) \odot \Sigma(Q)$ 를 만족한다. 이러한 $R$ 을 $P \boxdot Q$ 라 한다.
이를 증명하기 위해 두 Lemma가 필요하다.
Lemma 8.1. 행렬 $\Sigma(R)$에 대해, 순열 $R$ 이 존재할 조건은 다음과 동치이다:
- $\Sigma(R)_{i, 1} = 0$
- $\Sigma(R)_{N+1, i} = 0$
- $\Sigma(R)_{i, N+1} = N + 1 - i$
- $\Sigma(R)_{1, i} = i - 1$
- $\Sigma(R){i, j} - \Sigma(R){i, j-1} - \Sigma(R){i+1, j} + \Sigma(R){i+1, j-1} \geq 0$
Proof of Lemma 8.1. 순열을 복원할 조건은 부분합의 역연산인 "변홧값 배열" 에서, 각 행과 열에 정확히 하나의 $1$ 이 존재하고 그 외 모든 원소가 $0$ 임과 동치이다. 5번째 식은 모든 원소가 음이 아님을 보장한다. 3/4번째 식은 모든 행과 열의 합이 $1$ 임을 보장한다. $\blacksquare$
Lemma 8.2. 임의의 행렬 $A$에 대해, $A_{i, j} - A_{i, j-1} - A_{i+1, j} + A_{i+1, j-1} \geq 0$ 가 모든 $i, j$ 에 대해 만족하는 것은 $A_{i_1, j_2} - A_{i_1, j_1} - A_{i_2, j_2} + A_{i_2, j_1} \geq 0$ 가 모든 $i_1 \le i_2, j_1 \le j_2$ 에 대해 만족하는 것과 동치이다.
Proof of Lemma 8.2. $\rightarrow$ 는 수학적 귀납법을 사용하면ㄷ ㅗ니다. $\leftarrow$ 은 자명하다. $\blacksquare$
Proof of Theorem 8. Lemma 8.1의 첫 4개 항목을 증명한다. $\Sigma(P), \Sigma(Q)$ 의 모든원소가 $0$ 이상이기 때문에 $\Sigma(R)$ 역시 모든 원소가 $0$ 이상임을 관찰하라.
- $\Sigma(R){i, 1} \le \Sigma(P){i, 1} + \Sigma(Q)_{1, 1} = 0$
- $\Sigma(R){N+1, i} \le \Sigma(P){N+1, N+1} + \Sigma(Q)_{N+1, i} = 0$
- $\Sigma(R){i, N + 1} = \min(\Sigma(P){i, j} + \Sigma(Q){j, N+1}) = \min(\Sigma(P){i, j} + N+1-j)$. 변홧값을 관찰하면 항이 $j = N + 1$ 에서 최소화됨을 볼 수 있다. $\Sigma(R){i, N+1} = \Sigma(P){i, N+1} = N+1-i$
- $\Sigma(R){1, i} = \min(\Sigma(P){1, j} + \Sigma(Q){j, i}) = \min(j-1 + \Sigma(Q){j, i})$. 변홧값을 관찰하면 항이 $j = 1$ 에서 최소화됨을 볼 수 있다. $\Sigma(R){1, i} = \Sigma(Q){1, i} = i-1$
여기서 변홧값을 관찰한다 는 것은 다음과 같은 뜻이다. $0 \le \Sigma(P){i, j} - \Sigma(P){i, j - 1} \le 1$ 이 성립하기 때문에, $j$ 를 $1$ 늘릴 경우 위 값은 최대 $1$ 증가한다. 하지만, $N + 1 - j$ 는 $j$ 를 $1$ 늘릴 경우 무조건 $1$ 감소하니, 최소화를 위해 $j$ 를 늘리지 않을 이유가 없다. 이러한 논증을 이 글에서 반복적으로 사용할 것이니 익혀두면 좋다.
마지막 항목을 증명할 차례다. $k_1, k_2$ 를 $\Sigma(R){i, j} = \Sigma(P){i, k_1} + \Sigma(Q){k_1, j}$, $\Sigma(R){i+1, j-1} = \Sigma(P){i+1, k_2} + \Sigma(Q){k_2, j-1}$ 가 만족되는 인덱스라고 하자. $k_1 \le k_2$ 라고 하면 다음이 성립한다.
$\Sigma(R){i, j-1} + \Sigma(R){i+1, j}$
$= \min_k (\Sigma(P){i, k} + \Sigma(Q){k, j-1}) + \min_k (\Sigma(P){i+1, k} + \Sigma(Q){k, j})$
$\le \Sigma(P){i, k_1} + \Sigma(P){i+1, k_2} + \Sigma(Q){k_1, j-1} + \Sigma(Q){k_2, j}$
$\le \Sigma(P){i, k_1} + \Sigma(P){i+1, k_2} + \Sigma(Q){k_1, j} + \Sigma(Q){k_2, j-1}$ (Lemma 8.2)
$=\Sigma(R){i, j} + \Sigma(R){i+1, j-1}$
$k_1 \geq k_2$ 일 때도 동일하다. 이 때는 Lemma 8.2 를 $\Sigma(P)$ 에 사용한다. $\blacksquare$
Theorem 9. $\boxdot$ 연산자는 결합 법칙이 성립한다.
Proof. Min-plus 행렬 곱은 일반 행렬 곱처럼 결합 법칙이 성립한다. $\blacksquare$
Lemma 10. $I$ 를 identity permutation 이라고 할 때 ($I(i) = i$), $P \boxdot I = P$ (변홧값을 관찰하면 증명할 수 있다.) $\blacksquare$
이제 Seaweed와 $\boxdot$ 연산자의 동치를 보일 수 있는 최종 Theorem을 보일 준비가 되었다.
Theorem 11. $N$ 개의 seaweed와, 연산 수열 $i_1, i_2, \ldots, i_k$가 주어진다고 하자. 각 연산의 뜻은 다음과 같다:
- 초기에는 $i$ 번째 seaweed가 $i$ 번째 위치에 있다.
- 각 $1 \le x \le k$에 대해 순서대로, $i_x$ 위치에 있는 seaweed의 인덱스가 $i_x + 1$ 위치에 있는 seaweed보다 작을 경우 둘의 위치를 교환한다.
$P_i$ 를 위에서 정의한 기초 순열 이라고 하자. $P = P_{i_1} \boxdot P_{i_{2}} \boxdot \ldots \boxdot P_{i_k}$ 라고 할 때, 모든 연산 이후 $i$번째 seaweed 는 $P(i)$ 위치에 있다.
Proof of Theorem 11. $k$ 에 대한 귀납법을 사용한다. 귀납 가정에 의해 $P_{i_1} \boxdot P_{i_{2}} \boxdot \ldots \boxdot P_{i_{k-1}}$ 은 $k - 1$ 번의 연산 후 seaweed의 위치를 저장한다. 아래와 같이 정의하자:
- $t = i_k$
- $A = P_{i_1} \boxdot P_{i_{2}} \boxdot \ldots \boxdot P_{i_{k-1}}$
- $B = P_{i_1} \boxdot P_{i_{2}} \boxdot \ldots \boxdot P_{i_{k}}$
- $A(k_0) = t, A(k_1) = t+1$
다음 명제를 증명하면 된다:
- $B(k_0) = t+1, B(k_1) = t, B(i) = A(i)$ for all other $i$ if $k_0 < k_1$
- $B= A$ if $k_0 > k_1$
이는 다음과 동치이다:
- $\Sigma(B){i, j} = \Sigma(A){i, j} + 1$ if $k_0 < i \le k_1, j = t + 1$
- $\Sigma(B){i, j} = \Sigma(A){i, j}$ otherwise.
$\Sigma(P_t) - \Sigma(I)$ 에 있는 0이 아닌 항은 $(\Sigma(P_t) - \Sigma(I))_{t+1, t+1} = 1$ 뿐이다. $\Sigma(A) \odot \Sigma(I) = \Sigma(A)$ 이기 때문에, $\Sigma(B)$ 와 $\Sigma(A)$ 는 $t+1$ 번 열에서만 값이 달라진다. $t + 1$ 번 열에서는:
$\Sigma(B){i, t + 1}$
$= \min_j (\Sigma(A){i, j} + \Sigma(P_t){j, t + 1})$
$= \min(\min{j \le t} (\Sigma(A){i, j} + t + 1 - j), \Sigma(A){i, t + 1} + 1, (\min_{j > t+1} \Sigma(A){i, j})$
$= \min(\Sigma(A){i, t} + 1,\Sigma(A)_{i, t + 2})$ (변홧값)
$k_0 < k_1$ 일 경우:
- $\Sigma(A){i, t} = \Sigma(A){i, t + 1} - 1 = \Sigma(A)_{i, t + 2} - 2$ ($i \le k_0$)
- $\Sigma(A){i, t} = \Sigma(A){i, t + 1} - 0 = \Sigma(A)_{i, t + 2} - 1$ ($k_0 < i \le k_1$)
- $\Sigma(A){i, t} = \Sigma(A){i, t + 1} - 0 = \Sigma(A)_{i, t + 2} - 0$ ($k_1 < i$)
$\Sigma(B){i, t+1} = \Sigma(A){i, t+1} + 1$ iff $k_0 < i \le k_1$ 임을 관찰할 수 있다.
$k_0 > k_1$ 일 경우:
- $\Sigma(A){i, t} = \Sigma(A){i, t + 1} - 1 = \Sigma(A)_{i, t + 2} - 2$ ($i \le k_1$)
- $\Sigma(A){i, t} = \Sigma(A){i, t + 1} - 1 = \Sigma(A)_{i, t + 2} - 1$ ($k_1 < i \le k_0$)
- $\Sigma(A){i, t} = \Sigma(A){i, t + 1} - 0 = \Sigma(A)_{i, t + 2} - 0$ ($k_0 < i$)
$\Sigma(B){i, t+1} = \Sigma(A){i, t+1}$ 임을 관찰할 수 있다. $\blacksquare$
Part 2
Part 1에서는 문제를 해결하기 위한 모든 기초 이론을 짚고 넘어갔다. Part 1에 있는 내용을 그대로 구현할 경우 $O(N^5 + Q \log N)$ 시간에 Range LIS를 구할 수 있는데, 이것으로는 물론 문제를 해결하기 너무 느리니 다음 글에서 이를 단계적으로 $O(N \log^2 N + Q \log N)$ 으로 줄여나갈 것이다. 우리는 또한 이 테크닉을 사용하여 풀 수 있는 문제들을 더 자세히 살펴볼 것이다.
Practice problem
'공부 > Problem solving' 카테고리의 다른 글
| 2023.08.13 problem solving (0) | 2023.08.13 |
|---|---|
| 구간 최장 증가 부분 수열 쿼리 (Part 2) (0) | 2023.02.11 |
| Suffix Automaton (0) | 2023.01.08 |
| SMAWK algorithm as an alternative for D&C optimization (0) | 2023.01.01 |
| Good Bye 2022 짧은 후기 (0) | 2022.12.31 |
- Total
- Today
- Yesterday
