티스토리 뷰
이 글에서는 Monika Henzinger, Andrea Lincoln, Stefan Neumann, Virginia Vassilevska Williams의 Conditional Hardness for Sensitivity Problems 라는 논문을 요약한다.
이론 전산에서 Dynamic algorithm은, 입력 데이터에 작은 변화가 점진적으로 가해지더라도 데이터에 대해 물어볼 수 있는 특정한 문제들의 답을 그대로 보존하는 알고리즘을 뜻한다. 예를 들어서, 그래프의 "연결성" (connectivity) 를 보존하는 dynamic algorithm은 입력 그래프에 간선 추가와 제거가 이루어질 때 $s - t$ 간에 경로가 있는지 여부의 쿼리를 반환할 수 있다. 최근 이루어진 여러 연구를 통해서 Dynamic algorithm에 대해서 Conditional lower bound가 많이 증명되었고, 이를 통해서 어떠한 문제는 특정한 추측 (conjecture) 가 깨지지 않는 한 Dynamic algorithm을 통해서 효율적으로 해결할 수 없음이 증명되었다.
이러한 문제점을 해결하기 위해서 Dynamic algorithm을 조금 더 제한된 환경에서 해결하고자 하는 시도들이 등장하였는데, 그 중 하나는 입력 데이터에 가해질 수 있는 최대 변화량을 제한하는 시도이다. 이러한 알고리즘들을 sensitivity data structure 라고 부르며, 목표는 Sensitivity의 가정 하에 Dynamic algorithm의 conditional lower bound보다 빠른 알고리즘을 얻는 것이다.
엄밀히 말해, Sensitivity가 $d$ 인 자료 구조는 다음과 같은 연산을 지원한다:
- Update: $d$ 개의 변경을 초기 자료 구조에 수행한 것을 현재 상태로 둔다 (예를 들어, 간선 $d$ 개 추가 혹은 제거)
- Query: 사용자가 자료 구조의 현재 상태에 대해서 질의를 한다.
Decremental connectivity 문제를 예시로 들어보자. Decremental connectivity 문제를 해결하는 Dynamic algorithm은 간선 제거 쿼리와, 두 정점 간에 경로가 있는지를 판별하는 쿼리만을 받을 것이다. 반면, $d = 1$ 일 때 이 문제에 대한 sensitivity data structure 는, 간선 하나가 제거된 상태에서 두 정점 간에 경로가 있는지를 판별하는 문제가 된다. 이 문제는 그래프의 절선을 구한 후 이중 연결 요소를 계산해 주면 풀 수 있다. 위 예시는 Dynamic algorithm에 비해 Sensitivity algorithm이 간단함을 보여준다. 또한 Sensitivity라는 것이 낯선 개념이 아니고, 절점/절선과 같이 이미 통용되던 개념을 Dynamic algorithm의 컨텍스트에서 다시 분석한 것일 뿐임을 보여준다.
이 논문에서는 몇 가지 유명한 가설들을 사용해서 아주 많은 Sensitivity algorithm에 대한 새로운 Conditional lower bound를 보인다. 즉, Sensitivity라는 새로운 분야에서 Conditional hardness를 보이는 좋은 템플릿을 소개한다. 이러한 템플릿들을 익힘으로서, Sensitivity algorithm에 대한 통찰을 늘리고, 이후 이 분야에 새로운 문제가 연구될 때 Hardness를 보이는 과정에서 참고할 만한 자료가 될 수 있을 것이라고 생각한다. PS를 통해서 알고리즘을 배울 때도 일반적으로 효율적인 알고리즘을 배우지 Hardness를 배우지는 않기 때문에, 실제 알고리즘 연구에 대한 통찰을 얻기에도 좋은 자료라고 생각이 된다.
논문에 나온 Hardness result가 정말 많은데, 그 중 중요도가 높은 것만 몇 개 추려서 소개한다.
1. BMM Conjecture를 사용한 Lower bound
다음과 같은 가설을 Boolean Matrix Multiplication (BMM) conjecture라 한다.
BMM Conjecture. 임의의 $\epsilon > 0$ 에 대해서, 두 $n \times n$ 불리언 행렬의 곱을 $O(n^{3 - \epsilon})$ 시간 (랜덤 알고리즘일 경우, 시간 기댓값) 에 계산하는 조합적 (combinatorial) 알고리즘은 존재하지 않는다.
위 가설을 보고 의아하게 느낄 수 있는 사람들이 많을 것 같다. 불리언 여부와 무관하게 두 $n \times n$ 행렬의 곱을 $O(n^{2.373})$ 시간에 계산할 수 있기 때문이다. BMM Conjecture의 자세한 내용에 대해서는 다음 블로그 글에서 설명할 예정이다. 일단 이 글에서는 위가 사실이라고 단순하게 가정하고 넘어간다. BMM Conjecture이 참이라면, 다음 사실이 성립한다:
Triangle Conjecture. $n$ 개의 정점이 있는 무향 그래프에서, 조합적 알고리즘을 사용하여 삼각형 (3-cycle) 을 찾는데 최소 $n^{3 - o(1)}$ 시간이 사용된다.
1.1 BMM Conjecture 하의 Decremental diameter
Theorem. Triangle Conjecture가 참일 경우, 임의의 $\epsilon > 0$ 에 대해, 전처리 $O(n^{3 - \epsilon})$, 업데이트 / 쿼리 $O(n^{2 - \epsilon})$ 시간에 Decremental $(4/3-\epsilon)$ approx. diameter를, sensitivity가 1일 때, 무방향 무가중치 그래프에서 조합적 알고리즘으로 해결할 수 없다.
아래 단락에서 이를 증명한다. 정확히는, 위 정리의 대우명제를 증명한다.
Decremental $(4/3-\epsilon)$ approx. diameter를, sensitivity가 1일 때 해결할 수 있다고 하자. 다음과 같은 그래프를 구성한 후, 해당 Sensitivity algorithm을 이로 초기화할 것이다.
- 정점 집합 $V$ 의 복사본 4개를 만들어, $V_1, V_2, V_3, V_4$ 라 하자.
- 모든 $1 \le i \le 3$ 에 대해 $(u, v) \in E$ 일 경우 $u_i \in V_i$ 과 $v_{i + 1} \in V_{i + 1}$ 를 잇는 무향 간선을 만든다.
- 각 정점 $v \in V$ 에 대해 두 정점 $a_v, b_v$ 를 만든다. $A = {a_v v \in V}, B = {b_v v \in V}$ 라 하자.
- $A$ 의 서로 다른 두 정점 사이를 무향 간선으로 이어 클리크를 만든다. $B$ 에 대해서도 동일하게 한다.
- 모든 $v \in V$ 에 대해, 간선 $(v_1, a_v)$, $(a_v, b_v)$ 를 추가한다.
- 모든 $v \in B, w \in V_4$ 에 대해, 간선 $(v, w)$ 를 추가한다.
- $c$ 라는 노드를 추가하여, 모든 $w \in (V_2 \cup V_3 \cup A)$ 에 대해 간선 $(c, w)$ 를 추가한다.
- $d$ 라는 노드를 추가하여, 모든 $w \in (V_3 \cup V_4 \cup B)$ 에 대해 간선 $(d, w)$ 를 추가한다.
- 마지막으로, $c$ 와 $d$ 를 잇는 간선을 추가한다.
아래 사진은 위에서 설명한 그래프를 도식화한 것이다.

이 그래프에서 임의의 두 정점을 잇는 최단 거리는 항상 $3$ 이하임을 관찰하자. 기본적으로 아래에 깔려 있는 사이클을 사용하면 $1 + 4/2 + 1 = 4$ 이하이고, $4$ 인 경우도 잘 따져보면 없기 때문이다. 만약 $B$ 와 $V_4$ 를 잇는 간선들이 모두 없어진다면, $V_1 \times V_4$ 를 잇는 최단 거리는 $3$ 이 아니라 $4$ 일 수 있지만, 그 외의 경우에는 여전히 최단 거리가 $3$ 이하로 유지된다. 또한, $V_1 \times V_4$ 를 잇는 최단 거리는 $2$ 이하일 수 없으니, 그래프의 지름은 $3$ 이다.
다음 Lemma를 사용한다.
Lemma. 모든 $v \in G$ 에 대해서, $G^\prime \setminus {(b_v, v_4)}$ 의 지름이 $3$ 이라는 것과, $G$ 에서 $v$ 를 포함한 삼각형이 있음이 동치이다.
Proof. 원래 그래프의 지름이 3이니, 지름이 4가 된다면, 이 지름의 한 끝은 $v_4$여야 한다. 또한, $v_4$ 에서 거리 $3$ 으로 갈 수 없는 점은 $v_1$ 뿐이니, $v_1$ 과 $v_4$ 사이의 경로만 보면 된다.
만약 $G$ 에서 $v$ 를 포함하는 삼각형 $(v, w, u)$ 가 있으면, ${v_1, w_2, u_3, v_4}$ 와 같은 경로가 $G^\prime \setminus {(b_v, v_4)}$ 에 존재한다.
만약 $G^\prime \setminus {(b_v, v_4)}$ 의 지름이 3이라면, $v_1$ 과 $v_4$ 사이에 길이 3의 경로가 존재한다. 이는 $A, B$를 거치는 형태로는 존재할 수 없다. 고로 ${v_1, w_2, u_3, v_4}$ 와 같은 형태여야 하고, 그러면 삼각형을 찾을 수 있다.
이제 다음과 같은 방법으로 삼각형을 찾을 수 있다.
- Decremental $(4/3-\epsilon)$ approx. diameter를 크기 $O(n)$ 의 그래프로 초기화한다.
- 원래 그래프의 모든 정점 $v \in V$ 에 대해, ${(b_v, v_4)}$ 간선을 제거하는 업데이트 후 지름을 찾는다. 지름이 $4$ 미만일 경우, 원래 그래프의 지름이 $3$ 이니, Lemma에 의해 삼각형이 존재한다. 고로 삼각형이 존재함을 결정한다.
- 모든 $v$에 대해 삼각형을 찾지 못했다면 삼각형이 존재하지 않음을 결정한다.
초기화에 $O(n^{3 - \epsilon})$, $n$ 번의 쿼리에 $O(n^{2 - \epsilon})$ 시간이 걸렸기 때문에, 삼각형 판별을 $O(n^{3 - \epsilon})$ 시간에 조합적으로 해결했다. 고로 Triangle Conjecture는 거짓이다. $\blacksquare$
1.2 BMM Conjecture 하의 Reachability
Theorem. Triangle Conjecture가 참일 경우, 임의의 $\epsilon > 0$ 에 대해, 전처리 $O(n^{3 - \epsilon})$, 업데이트 / 쿼리 $O(n^{2 - \epsilon})$ 시간에 다음 문제들을 조합적 알고리즘으로 해결할 수 없다. 그래프는 방향성이 존재한다.
- incremental s-t reachability with sensitivity $2$
- incremental s.s reachability with sensitivity $1$ (s.s는 single source의 약자)
- static a.p reachability (a.p는 all pair의 약자)
Proof. 대우명제를 증명하여, 각 문제들을 해결할 수 있을 때 Triangle Conjecture를 반증할 수 있음을 보인다. $G = (V, E)$ 를 삼각형을 찾게 될 그래프라고 하자. 다음과 같은 그래프 $G^\prime$ 을 구성한다.
- 정점 집합 $V$ 의 복사본 4개를 만들어, $V_1, V_2, V_3, V_4$ 라 하자.
- 모든 $1 \le i \le 3$ 에 대해 $(u, v) \in E$ 일 경우 $u_i \in V_i$ 과 $v_{i + 1} \in V_{i + 1}$ 를 잇는 방향 간선 $(u_i \rightarrow v_{i + 1})$ 을 만든다.
1.1에서 다룬 그래프의 단순화된 형태로, 이 그래프에서 $v$ 를 포함하는 삼각형이 존재하는 것과, $v_1 \rightarrow v_4$ 로 가는 경로가 존재함이 동치임을 관찰할 수 있다. 이제 명제를 모두 증명할 수 있다.
- incremental s-t reachability with sensitivity $2$ 가 해결된다고 하자. $G^\prime$ 에 두 정점 $s, t$ 를 추가하여 초기화하자. 모든 $v \in V$ 에 대해서 쿼리를 하는데, $(s \rightarrow v_1), (v_4 \rightarrow t)$ 간선을 추가한 후 $s \rightarrow t$ 간에 경로가 있는 지를 판별한다.
- incremental single source reachability with sensitivity $1$ 가 해결된다고 하자. $G^\prime$ 에 정점 $s$ 를 추가하여, $s$ 를 source로 두고 초기화하자. 모든 $v \in V$ 에 대해서 쿼리를 하는데, $(s \rightarrow v_1)$ 간선을 추가한 후 $s \rightarrow v_4$ 간에 경로가 있는 지를 판별한다.
- static a.p reachability가 해결된다고 하자. 모든 $v \in V$ 에 대해서 쿼리를 하는데, $v_1 \rightarrow v_4$ 간에 경로가 있는 지를 판별한다.
모든 경우에 대해서 한 번의 초기화, $n$ 번의 업데이트 / 쿼리가 있었다. 고로 이 중 하나라도 해결된다면 Triangle Conjecture가 반증된다.
1.3 BMM Conjecture 하의 Shortest paths
Theorem. Triangle Conjecture가 참일 경우, 임의의 $\epsilon > 0$ 에 대해, 전처리 $O(n^{3 - \epsilon})$, 업데이트 / 쿼리 $O(n^{2 - \epsilon})$ 시간에 다음 문제들을 무방향 무가중치 그래프에서 조합적 알고리즘으로 해결할 수 없다.
- $(7/5-\epsilon)$ approx s-t shortest paths with sensitivity $2$
- $(3/2-\epsilon)$ approx s.s shortest paths with sensitivity $1$
- static $(5/3 - \epsilon)$ a.p reachability
Proof. 대우명제를 증명하여, 각 문제들을 해결할 수 있을 때 Triangle Conjecture를 반증할 수 있음을 보인다. $G = (V, E)$ 를 삼각형을 찾게 될 그래프라고 하자. 다음과 같은 그래프 $G^\prime$ 을 구성한다.
- 정점 집합 $V$ 의 복사본 4개를 만들어, $V_1, V_2, V_3, V_4$ 라 하자.
- 모든 $1 \le i \le 3$ 에 대해 $(u, v) \in E$ 일 경우 $u_i \in V_i$ 과 $v_{i + 1} \in V_{i + 1}$ 를 잇는 가중치 1의 무방향 간선 $(u_i, v_{i + 1})$ 을 만든다.
1.2의 그래프와 거의 동일하다. 이제 명제를 증명한다.
- $v_1, v_4$ 간의 최단 거리는 $3$ 이상이며, 이분 그래프이기 때문에 홀수이다. $(s, v_1), (v_4, t)$ 간선을 추가한 후 $s \rightarrow t$ 간에 경로가 $5$ 인지 $7$ 이상인지를 $(7/5 - \epsilon)$ approx s - t shortest path로 판별한다.
- 동일하게, $(s, v_1)$ 간선을 추가한 후 $s - t$ 간에 경로가 $4$ 인지 $6$ 이상인지를 $(3/2 - \epsilon)$ approx s.s shortest path로 판별한다.
- $v_1 - v_4$ 간에 경로가 $3$ 인지 $5$ 이상인지를 $(5/3 - \epsilon)$ a.p reachability로 판별한다.
모든 경우에 대해서 한 번의 초기화, $n$ 번의 업데이트 / 쿼리가 있었다. 고로 이 중 하나라도 해결된다면 Triangle Conjecture가 반증된다.
2. APSP Conjecture 하의 Lower bound
다음과 같은 가설을 APSP (All Pair Shortest Paths) Conjecture라 한다.
APSP Conjecture. $n$ 개의 간선, $poly(n)$ 이하의 양의 정수 가중치를 가진 $m$ 개의 간선이 주어졌을 때, 모든 쌍 최단 경로 문제 (All Pair Shortest Paths) 는 임의의 $\epsilon > 0$ 에 대해서 $O(n^{3 - \epsilon})$ 보다 빠르게 (랜덤 알고리즘일 경우, 시간 기댓값) 해결할 수 없다.
모든 쌍 최단 경로 문제는 Floyd-Warshall을 사용하여 $O(n^3)$ 에 푸는 방법이 잘 알려져 있다. 이것보다 빠른 알고리즘이 존재하지 않는다는 것이 APSP Conjecture의 뜻이다. 이 글에서는 이를 통해서 증명할 수 있는 세 가지 Hardness를 소개한다.
Theorem. APSP Conjecture 가 참일 경우, 임의의 $\epsilon > 0$ 에 대해, 전처리 $O(n^{3 - \epsilon})$, 업데이트 / 쿼리 $O(n^{2 - \epsilon})$ 시간에 다음 문제들을 해결할 수 없다.
- decremental s-t shortest paths in dir. weighted graphs with sensitivity $1$
- decremental s-t shortest paths in undir. weighted graphs with sensitivity $2$
- decremental diameter in undir. weighted graphs with sensitivity $1$
이를 위해서 우리는 다음과 같은 정리를 사용한다.
Theorem. APSP Conjecture가 참일 경우, 가중치 합이 음수인 삼각형의 존재 여부를 $O(n^{3 - \epsilon})$ 보다 빠르게 판별할 수 없다.
증명은 Subcubic Equivalences Between Path, Matrix, and Triangle Problems 논문을 참조하라.
Corollary. APSP Conjecture가 참일 경우, 가중치 합이 최소인 삼각형을 $O(n^{3 - \epsilon})$ 보다 빠르게 찾을 수 없다.
2.1 APSP Conjecture 하의 Directed Shortest Paths
아래 내용은 사실 이 논문의 Contribution은 아니고, 위에 링크한 논문에서 증명된 내용이다. 하지만 완결성을 위해 증명을 소개한다.
다음 사실을 관찰하자.
Lemma. decremental s-t shortest paths in dir. weighted graphs with sensitivity $1$ 를 전처리 $O(n^{3 - \epsilon})$, 업데이트 / 쿼리 $O(n^{2 - \epsilon})$ 시간에 해결할 수 있다면, 그래프의 s-t second shortest simple path를 $O(n^{3 - \epsilon})$ 에 해결할 수 있다.
Proof. 그래프의 $s - t$ shortest path를 아무거나 하나 찾는다. 이는 $O(n^2)$ 시간에 할 수 있다. second shortest path는 이 경로에서 하나 이상의 간선을 포함하지 않는 최단 경로와 동일하다. 고로 최단 경로를 이루는 최대 $O(n)$ 개의 간선들을 하나씩 지우는 업데이트를 하고, 최단 경로를 쿼리하면 된다.
이제 Main Theorem을 소개한다.
Theorem. $T(n)$ 시간에 $n$ 개의 정점을 가진 가중치 있는 유향 그래프에서 s-t second shortest simple path를 계산할 수 있다고 하자. 그렇다면, $T(O(n))$ 시간에 $n$ 개의 정점을 가진 그래프에서 최소 가중치 삼각형을 해결할 수 있다.
Proof. $G$ 를 최소 가중치 삼각형을 해결할 인스턴스라고 하자. 일반성을 잃지 않고, $G$ 가 완전 그래프라고 하자 (간선이 없는 곳에 아주 큰 가중치의 간선 추가) $n$ 개의 정점을 가진다고 할 때, 다음과 같이 그래프를 구성하자.
- $n + 1$ 개의 정점을 가진 경로 $P = p_0 \rightarrow p_1 \rightarrow p_n$ 을 만든다. 모든 간선 $p_i \rightarrow p_{i + 1}$ 의 가중치는 $0$ 이다.
- $3 \times n$ 개의 정점 $A = {a_1, \ldots, a_n}, B = {b_1, \ldots, b_n}, C = {c_1, \ldots, c_n}$ 을 만든다.
- 모든 $i, j \in [n]$ 에 대해 가중치가 $w(i, j)$ 인 간선 $(a_i \rightarrow b_j), (b_i \rightarrow c_j)$ 를 추가한다.
- $W^\prime$ 를 $G$ 에서 등장한 최대 가중치라고 하고, $W = 3W^\prime + 1$ 이라 하자.
- 모든 $j \in [n]$ 에 대해, 가중치가 $jW$ 인 간선 $(c_j \rightarrow p_j)$ 을 추가한다.
- 모든 $0 \le i \le n - 1, 1 \le r \le n$ 에 대해, 가중치 $(n - i - 1)W + w(i + 1, r)$ 인 간선 $(p_i \rightarrow a_r)$ 을 추가한다.
이제 $s = p_0, t = p_n$ 이라고 두자. 이 그래프의 s-t 최단 경로는 $P$ 이며, 모든 간선 가중치가 양수이기 때문에 이것이 유일하다. 두 번째 최단 경로는 $P$ 에서 벗어나 $a_i, b_j, c_t$ 를 거친 후 다시 $P$ 로 돌아올 것인데, 이 때의 가중치는 $(n - s - 1)W + w(s+1, i) + w(i, j) + w(j, t) + tW$ 임을 볼 수 있다.
여기서 두번째 최단 경로는 무조건 $t = s + 1$ 을 만족해야 함을 관찰하자. 경로가 단순하기 때문에 자명히 $t > s$ 여야 하고, $t = s + 2$ 일 경우 $W$ 만큼 추가 비용이 부과되기 때문에 최적일 수 없다. 그래프가 완전 그래프이기 때문에 $t = s + 1$ 인 두번째 최단 경로 역시 존재한다.
고로, 두 번째 최단 경로의 비용은 어떠한 $a_i, b_j, c_t$ 에 대해 $nW + w(t, i) + w(i, j) + w(j, t)$ 를 만족한다. 고로 두 번째 최단 경로에 대응되는 삼각형이 존재하며, 모든 삼각형은 최단 경로는 아닌 단순 경로에 대응된다. $nW$ 는 상수이니, 두 번째 최단 경로의 비용을 최소화하면 삼각형의 비용 역시 최소화된다. $\blacksquare$
2.2 APSP Conjecture 하의 Undirected Shortest Paths
무방향 그래프에서는 sensitivity가 $1$ 일 때 decremental s-t shortest paths를 효울적으로 푸는 알고리즘이 사실 존재하며 경시 대회 문제로도 알려져 있다. 고로 $1$ 일 때는 해결할 수 있지만, $2$ 가 되면 어려워지는 알고리즘이라고 볼 수 있다. 이 단락에서는 sensitivity가 $2$ 일 때 decremental s-t shortest paths를 효울적으로 푸는 알고리즘이 존재한다면, 이를 통해서 가중치 합이 음수인 삼각형을 판별할 수 있는 알고리즘을 만들 수 있다는 것을 증명한다.
먼저 입력 그래프에 음수 간선이 없다면 No를 판별하자. $M$ 이 그래프의 최소 가중치라면, 모든 간선에 $-M+1$ 을 더해서 간선의 가중치를 전부 양수로 만들고, $-3M+3$ 미만의 가중치를 가지는 삼각형을 판별하는 문제로 변환한다.
$W^\prime$ 를 $G$ 에서 등장한 최대 가중치라고 하고, $W = 6W^\prime + 1$ 이라 하자.
아래와 같이 그래프를 구성하자.
- $n + 1$ 개의 정점을 가진 경로 $P = {p_0, p_1, \ldots, p_n}$ 을 만든다. 모든 간선 $(p_i, p_{i + 1})$ 의 가중치는 $0$ 이다.
- $n + 1$ 개의 정점을 가진 경로 $Q = {q_0, q_1, \ldots, q_n}$ 을 만든다. 모든 간선 $(q_i, q_{i + 1})$ 의 가중치는 $0$ 이다.
- $3 \times n$ 개의 정점 $A = {a_1, \ldots, a_n}, B = {b_1, \ldots, b_n}, C = {c_1, \ldots, c_n}$ 을 만든다.
- 모든 $i, j \in [n]$ 에 대해 가중치가 $w(i, j) + 6nW$ 인 간선 $(a_i, b_j), (b_i, c_j)$ 를 추가한다.
- 모든 $j \in [n]$ 에 대해, 가중치가 $(7n-j)W$ 인 간선 $(c_j, q_j)$ 을 추가한다.
- 모든 $i, j \in [n]$ 에 대해, 가중치 $(7n-j)W + w(i, j)$ 인 간선 $(p_j, a_i)$를 추가한다.
- $s = p_0, t = q_0$ 으로 둔다.
아래 사진은 위에서 설명한 그래프를 도식화한 것이다. Notation이 조금 다르니 그림만 보자.
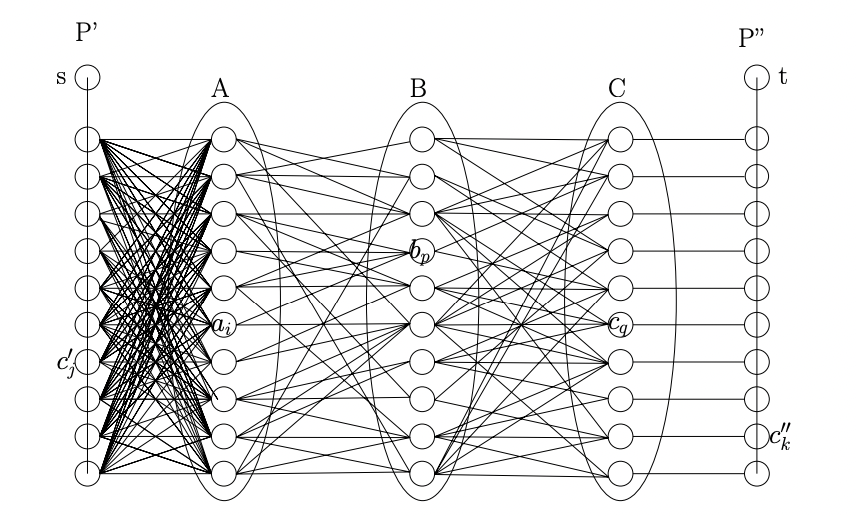
그래프에 있는 모든 간선의 가중치는 $0$ 이거나, $[6nW, 7nW + W/6]$ 구간 안에 있음을 관찰하면 좋다.
이제 다음과 같이 쿼리를 하자.
- 모든 $i \in [n]$ 에 대해, 간선 $(p_i, p_{i + 1})$ 과 간선 $(q_i, q_{i + 1})$ 을 제거한다. 만약 $i = n$ 일 경우 아무것도 지우지 않는다.
- $s - t$ 최단 경로를 찾는다.
이 경우 생기는 최단 경로에 대해서 관찰하자.
- 먼저, 최단 경로를 이루는 간선 중, $0$ 초과 가중치를 가지는 간선은 $4$ 개이다. $4$ 개 의 간선으로 이루어진 경로가 항상 존재하며, 그렇지 않을 경우 이분 그래프라 간선의 개수가 $6$개 이상인데, $(7nW + W/6) \times 4 < 6 \times 6nW$ 이기 때문에 이는 최적이 아니다.
- 최단 경로에서, 0 초과 가중치로 이루어진 경로 부분을 ${p_j, a_x, b_y, c_k, q_k}$ 라 하자. 이 경로의 길이는 $(7n-j)W + w(x, j) + w(x, y) + 6nW + w(y, k) + 6nW + (7n - k)W$ 이다.
- $x, y$ 를 고정했을 때, $W$ 값이 아주 크기 때문에 $j, k$ 를 최대화해야 한다. 지워진 간선에 의해 이 값은 모두 $i$ 이하여야 하고, 그래프가 완전 그래프이기 때문에 이 값들은 모두 $i$ 에서 형성될 수 있다.
- 이 경우 경로의 길이는 $(7n-i)W + w(x, i) + w(x, y) + 6nW + w(y, i) + 6nW + (7n - i)W$ 가 된다. 상수항을 제거하면 $i$ 를 포함하는 최소 크기 삼각형의 크기를 알 수 있다.
고로 한 번의 초기화, $n$ 번의 업데이트 / 쿼리를 통해 음수 삼각형의 존재를 판별할 수 있었다. 즉, sensitivity가 $2$ 일 때 decremental s-t shortest paths를 효울적으로 푸는 알고리즘이 존재한다면, APSP Conjecture가 반증된다.
2.3 APSP Conjecture 하의 Decremental Diameter
이 단락에서는 sensitivity가 $1$ 일 때 decremental diameter를 효울적으로 푸는 알고리즘이 존재한다면, 이를 통해서 가중치 합이 음수인 삼각형을 판별할 수 있는 알고리즘을 만들 수 있다는 것을 증명한다. 1.1 단락에서 구성한 그래프와 상당히 유사함을 관찰하면 좋다 (BMM Conjecture로의 Reduction은 전반적으로 APSP Conjecture로의 Reduction과 유사한 형식을 띄는 경우가 많다.)
그래프의 간선 가중치 범위가 $[-M, M]$ 사이라면, 모든 간선에 $5M$ 을 더해서 간선의 가중치를 전부 $[4M, 6M]$ 사이의 양수로 만들자. 또한, 간선이 없는 곳에 아주 큰 가중치의 간선을 추가해서 그래프를 완전 그래프로 만들자.
다음과 같이 그래프를 구성하여 Decremental Diameter 인스턴스에 초기화하자.
- 정점 집합 $V$ 의 복사본 4개를 만들어, $V_1, V_2, V_3, V_4$ 라 하자.
- 모든 $1 \le i \le 3$ 에 대해 $(u, v) \in E$ 일 경우 $u_i \in V_i$ 과 $v_{i + 1} \in V_{i + 1}$ 를 잇는 무향 간선을 만든다. 간선의 가중치는 $w(u, v)$ 이다.
- 각 정점 $v \in V$ 에 대해 두 정점 $a_v, b_v$ 를 만든다. $A = {a_v v \in V}, B = {b_v v \in V}$ 라 하자.
- $A$ 의 서로 다른 두 정점 사이를 무향 간선으로 이어 클리크를 만든다. $B$ 에 대해서도 동일하게 한다. 간선의 가중치는 $4M$ 이다.
- 모든 $v \in V$ 에 대해, 간선 $(v_1, a_v)$, $(a_v, b_v)$ 를 추가한다. 간선의 가중치는 $4M$ 이다.
- 모든 $v \in B, w \in V_4$ 에 대해, 간선 $(v, w)$ 를 추가한다. 간선의 가중치는 $4M$ 이다.
- $c$ 라는 노드를 추가하여, 모든 $w \in (V_2 \cup V_3 \cup A)$ 에 대해 간선 $(c, w)$ 를 추가한다. 간선의 가중치는 $4M$ 이다.
- $d$ 라는 노드를 추가하여, 모든 $w \in (V_3 \cup V_4 \cup B)$ 에 대해 간선 $(d, w)$ 를 추가한다. 간선의 가중치는 $4M$ 이다.
- 마지막으로, $c$ 와 $d$ 를 잇는 간선을 추가한다. 간선의 가중치는 $4M$ 이다.
1.1과 동일한 이유에 의해 이 그래프에서 항상 임의의 두 점을 잇는 길이 $12M$ 이하의 경로가 있음을 관찰하면 좋다.
다음 Lemma를 사용한다.
Lemma. 모든 $v \in G$ 에 대해서, $G^\prime \setminus {(b_v, v_4)}$ 의 지름이 $15M$ 미만이라는 것과, $G$ 에서 $v$ 를 포함한 가중치 합 음수 삼각형이 있음이 동치이다.
Proof. 원래 그래프의 지름이 $12M$이니, 지름이 $12M$ 초과가 된다면, 이 지름의 한 끝은 $v_4$여야 한다. 또한, $v_4$ 에서 거리 $12M$ 으로 갈 수 없는 점은 $v_1$ 뿐이니, $v_1$ 과 $v_4$ 사이의 경로만 보면 된다.
만약 $G$ 에서 $v$ 를 포함하는 가중치 $0$ 미만의 삼각형 $(v, w, u)$ 가 있으면, ${v_1, w_2, u_3, v_4}$ 와 같은 경로가 $G^\prime \setminus {(b_v, v_4)}$ 에 존재하며, 이 때의 길이는 $15M$ 미만이다.
만약 $G^\prime \setminus {(b_v, v_4)}$ 의 지름이 $15M$ 미만이라면, 지름을 이루는 간선은 $3$ 개 이하여야 하며, 그러한 경로는 무조건 $V_2, V_3$ 을 중점으로 거쳐야 한다. 고로, 지름이 $15M$ 미만이라면, 그 경로는 ${v_1, w_2, u_3, v_4}$ 와 같은 꼴을 띄고 있을 것이다. 이러한 경로는, 원래 그래프의 가중치 합 $0$ 미만의 삼각형에 대응된다.
이제 다음과 같은 방법으로 삼각형을 찾을 수 있다.
- Decremental diameter를 크기 $O(n)$ 의 그래프로 초기화한다.
- 원래 그래프의 모든 정점 $v \in V$ 에 대해, ${(b_v, v_4)}$ 간선을 제거하는 업데이트 후 지름을 찾는다. 지름이 $15M$ 미만일 경우, Lemma에 의해 음수 삼각형이 존재한다. 고로 음수 삼각형이 존재함을 결정한다.
- 모든 $v$에 대해 음수 삼각형을 찾지 못했다면 음수 삼각형이 존재하지 않음을 결정한다.
초기화에 $O(n^{3 - \epsilon})$, $n$ 번의 쿼리에 $O(n^{2 - \epsilon})$ 시간이 걸렸기 때문에, 음수 삼각형 판별을 $O(n^{3 - \epsilon})$ 시간에 조합적으로 해결했다. 고로 APSP Conjecture는 거짓이다. $\blacksquare$
'공부 > CS theory' 카테고리의 다른 글
| The Cut-Matching Game: Expanders via Max Flow (0) | 2023.05.12 |
|---|---|
| Introduction to APSP Conjecture and BMM Conjecture (0) | 2022.12.25 |
| Inapproximability in computational hardness (0) | 2022.11.01 |
| Shortest Cycle Through Specified Elements (0) | 2022.06.07 |
| Congestion Balancing (0) | 2022.06.02 |
- Total
- Today
- Yesterday
