티스토리 뷰
일반적인 그래프에서 효율적으로 해결할 수 있는 문제들을, 간선이 추가되고 제거되는 등의 업데이트가 가해질 때도 효율적으로 해결할 수 있는지를 연구하는 분야를 Dynamic Graph Algorithm이라고 부른다. 이 분야에 대해서는 최근 많은 연구가 진행되고 있으며, 여러 차례의 멤버십 글로도 이 분야의 다양한 최신 기술과 테크닉을 소개한 바 있다.
이 글에서 소개할 주제는 Decremental Graph Algorithm을 얻을 수 있는 프레임워크 중 하나인 Congestion Balancing 이다. 어떠한 알고리즘이 decremental하다는 것은, 간선 추가 쿼리는 처리할 수 없으나 제거 쿼리는 처리할 수 있다는 것을 뜻한다. Decremental algorithm 그 자체로는 실용적 가치가 존재하지 않다고 봐도 무방하다. 하지만 간선 추가/제거를 모두 다룰 수 있는 dynamic algorithm을 얻기 위해 decremental algorithm을 사용하는 경우는 상당히 많고 이러한 경우의 대표적인 예시로는 Dynamic MSF가 있다.
Congestion Balancing을 사용하면, 다음과 같은 문제들을 Decremental dynamic setting에서 해결할 수 있다.
- 방향 그래프에서 Reachability (두 정점 간에 경로가 있는지 판별) 및 SCC 관리 를 총 $mn^{2/3 + o(1)}$ 시간에 관리
- 방향 그래프에서 Single-source shortest path (최단 경로) 문제를 총 $n^{8/3 + o(1)}$ 시간에 해결
- 이분 그래프에서 $m \log^3 (n) / \epsilon^4$ 시간에 최대 매칭의 $(1 - \epsilon)$-approximation을 관리.
모두 그래프에서 아주 중요한 알고리즘들이며, 특히 Reachability, SCC, SSSP 문제의 경우 dynamic setting에서 해결하기 어려운 문제로 유명하다는 것이 큰 의외를 가진다. 이 문제들에 대해서는, 1981년 $O(nm)$ 에 해결하는 알고리즘이 나온 이후 학계에서 나온 첫 진전이다. 추가적으로, Congestion Balancing은 결정론적(deterministic) 알고리즘이기 때문에 랜덤 알고리즘보다 더 실용적 가치가 높다는 장점이 있다.
전체 논문이 굉장히 길 뿐만 아니라 어려운 개념들을 수반하기 때문에 (Expander decomposition, One-shot pruning, Cut-matching game 등) 노 베이스에서 설명하기 위해서는 선택과 집중이 필요하다고 생각한다. 위 세 문제 중 Congestion Balancing이라는 테크닉 하나로만 해결할 수 있는 문제는 이분 매칭 문제이며, 다른 문제들은 Expander decomposition 등을 통해서 플로우 문제로의 reduction 과정이 필요하다. 고로 이 글에서는 Congestion Balancing을 사용하여 이분 매칭을 효율적으로 해결하는 법에 집중한다.
Preliminaries
우리가 해결해야 할 문제는 다음과 같다:
- 가중치 없는 이분 그래프가 주어졌을 때, 간선 삭제 쿼리마다 최대 매칭의 $(1-\epsilon)$-appximation을 총 $O(m \log^3(n) / \epsilon^4)$ 시간에 관리하라.
편의상 $n$ 이 power of 2라고 가정한다. ($n = 2^k$ 인 음이 아닌 정수 $k$ 존재)
우리가 이 글에서 증명하게 될 Main Theorem은 다음과 같다.
Theorem 1. 무방향 무가중치 이분 그래프 $G = (L \cup R, E)$, 그리고 파라미터 $\mu \in [1, n], \epsilon \in (0, 1)$ 이 주어진다. 간선 삭제 쿼리와 함께 다음을 보장하는 알고리즘 RobustMatching 이 존재한다. 이 알고리즘의 시간 복잡도는 $O(m \log^2(n) / \epsilon^3)$ 시간이다.
- 알고리즘이 종료되는 시점에, $\mu(G) \le \mu(1 - \epsilon)$ 이 보장된다 ($\mu(G)$ 는 $G$ 의 최대 매칭의 크기를 뜻함).
- 알고리즘이 종료하기 전까지, $val(M) \geq \mu (1 - 5 \epsilon)$ 을 만족하는 fractional matching $M$ 을 관리한다.
Main Theorem을 사용하여 decremental 이분 매칭을 푸는 방법은 다음과 같다. 초기 $\mu = n$ 을 매칭의 크기로 두고, RobustMatching 이 매칭을 찾을 때까지 $\mu$ 를 $(1 - \epsilon)$ 배 한다. 매칭이 발견된 이후 간선 삭제 쿼리를 받는데, 간선 삭제 이후 알고리즘이 종료되었다면, 다시 매칭을 찾을 때까지 $\mu$ 를 $(1 - \epsilon)$ 배 하는 것을 반복한다. 이를 $\mu < 1$ 일 때까지 반복한다. 이 경우 항상 알고리즘은
- $val(M) \geq \mu(G) (1 - \epsilon) (1 - 5\epsilon) \geq \mu(G)(1 - 6\epsilon)$ 크기의 Fractional matching을 관리한다.
- $\mu$ 가 항상 $(1 - \epsilon)$ 배 감소하고, $(1 - \epsilon)^{\log n / \epsilon + 1} < 1$ 이니, RobustMatching 알고리즘을 $O(\log(n) / \epsilon)$ 번 호출한다.
마지막으로 Fractional matching은 일반적인 integral matching으로 dynamic하게 rounding할 수 있음이 알려져 있다 (Waj20). 이를 통해서 Theorem 1의 결과를 사용하면 decremental한 환경에서 이분 매칭을 관리할 수 있음을 관찰할 수 있다.
이후 내용은 모두 Theorem 1을 증명하는 것을 목표로 한다.
Failed attempts
Congestion balancing에 대한 직관을 얻기 위해, 몇 가지 나이브한 접근을 제시한다. 이 접근들은 모두 틀렸지만, 최종적인 congestion balancing의 근간이 되는 아이디어들을 포함한다.
Naive algorithm 1. 초기에 최대 매칭 $M$ 을 계산한다. 이후 $M$ 의 간선이 지워질 경우, 계속 지운다. 그러다가 $M$의 크기가 $(1 - \epsilon)$ 배 이하로 줄어들 경우, 다시 최대 매칭을 계산한다.
Countercase of 1. $K_{n, n}$ 과 같은 완전 이분 그래프를 생각해 보자. 쿼리로 최대 매칭에 속하는 간선들을 계속 지우면 재계산을 여러 번 해야 하지만, 그렇다고 $\mu(G)$ 가 줄어들지는 않는다.
이 알고리즘의 문제점은, 우리가 계산한 임의의 최대 매칭이 전체적인 최대 매칭을 과하게 대표 (overrepresent) 한다는 것이다. 실제로는 다른 형태의 최대 매칭도 존재하지만, 우리는 하나의 매칭만 가지고 있기 때문에 이러한 다른 최대 매칭으로 전환하는 데 시간이 걸린다.
이를 해결하기 위해 Fractional matching을 도입해서, 각각의 간선이 최대 매칭을 어느 정도 대변하는지 를 표현한다.
Naive algorithm 2. Fractional matching을 사용한다. 모든 간선에 작은 값을 적어서, 간선이 지워질 때도 fractional matching의 감소폭이 작게 유지되도록 보장한다. 예를 들어, $K_{n, n}$ 의 경우 모든 간선에 $\frac{1}{n}$ 이라는 값을 적을 경우 $M$ 의 크기가 $(1 - \epsilon)$ 배 이하로 줄어들기까지 오랜 시간이 걸린다.
Countercase of 2. 모든 최대 매칭에 속하는 간선들의 경우 작은 값을 적어서 매칭을 표현할 수 없다. 예를 들어, 최대 매칭이 유일할 경우 간선에는 모두 1이라는 큰 값이 적혀야 한다.
고로 각 간선에 적절한 값을 배정해서, 매칭을 어느 정도 대변하는 지를 잘 표현하면서도 쉽게 관리할 수 있도록 하는 것이 핵심이다. Congestion balancing 이라는 표현이 여기서 나온다. 각각의 간선에 배정된 값이 매칭의 congestion 을 잘 표현하도록 하며, 간선이 삭제되면서 이 congestion 을 적절히 balancing 하도록 하는 것이 목표이다.
Theorem 1의 증명: RobustMatching 알고리즘
이제 Congestion balancing의 목표를 이해했으니 몇가지 서브루틴을 소개한다. 이분 매칭을 해결할 때 일반적으로 사용하는 플로우 그래프는 다음과 같이 형성된다.
- Source에서 $L$ 의 모든 간선으로 $1$ 의 용량을 가진 간선을 잇고, $R$ 의 모든 정점에서 Sink로 $1$ 의 용량을 가진 간선을 잇는다.
- 각 간선을 $1$ 의 용량을 가진 방향 간선으로 바꾼다.
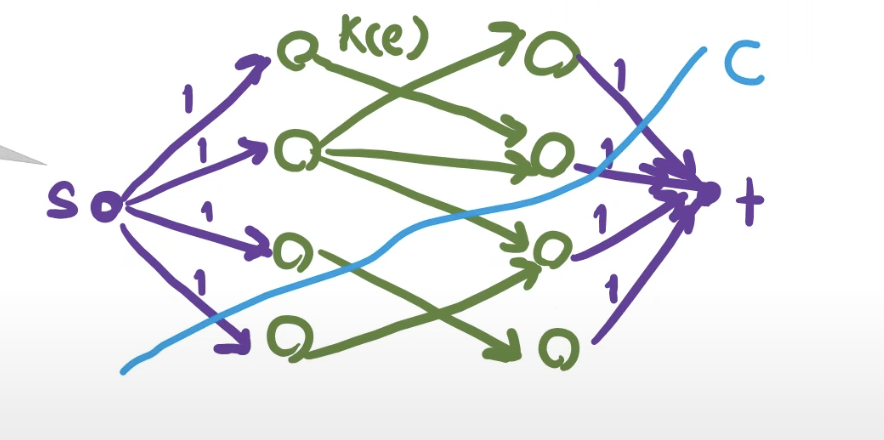
Congestion balancing도 이와 비슷하게 진행한다. 각각의 간선의 초기 congestion $\kappa(e)$ 이 있다고 하자. 다음과 같은 플로우 그래프를 만든다.
- Source에서 $L$ 의 모든 간선으로 $1$ 의 용량을 가진 간선을 잇고, $R$ 의 모든 정점에서 Sink로 $1$ 의 용량을 가진 간선을 잇는다.
- 각 간선을 $\kappa(e)$ 의 용량을 가진 방향 간선으로 바꾼다.
이 그래프의 최대 유량을 구하면 그것이 초기 이분 그래프의 fractional matching에 대응될 것이다. 또한, 최대 유량을 구할 경우, 이에 상응하는 컷 역시 구할 수 있다. 이 값을 사용하여 congestion balancing을 진행한다.
Theorem 2. Matching-Or-Cut 알고리즘은 $G = (L \cup R, E)$ 과 용량 함수 $\kappa : E \rightarrow R_{(0, 1]}, \mu \in [1, n], \epsilon \in (0, 1)$ 을 입력으로 받아 $O(m \log(n) / \epsilon)$ 시간에 둘 중 하나를 반환한다.
- $val(e) \le \kappa(e)$ 를 만족하는 크기 $\mu(1 - \epsilon)$ 의 fractional matching $M$
- $\kappa(S_L, R \setminus S_R) + |S_R| \le \mu + |S_L| - n$ 을 만족하는 두 집합 $S_L \subseteq L, S_R \subseteq R$
Proof. Bounded-height push-relabel이라는 것을 사용할 것이다. 이 부분의 대한 증명은 다음 챕터에서 진행한다.
아래 사진에서 컷 $C$의 왼쪽에 해당하는 집합이 $S_L, S_R$ 이라고 생각하면 이해하기 편하다.
Lemma 3. $O(m / \epsilon)$ 시간에 그래프에 $(1 - \epsilon)\mu(G)$ 이상의 최대 매칭을 찾을 수 있다.
Proof. Hopcroft-Karp로 $1/\epsilon$ 번 Blocking flow를 찾을 경우 반환되는 매칭이 $(1 - \epsilon)\mu(G)$ 이상임이 잘 알려져 있다. BOJ 18488 을 참조해도 좋다.
이제 Congestion Balancing을 사용한 RobustMatching 알고리즘을 소개한다.
Algorithm: Preprocess.
- 모든 $e \in E$ 에 대해 $\kappa(e) = 1/n$ 으로 설정한다.
- Initialize로 넘어간다.
Algorithm: Initialize
- 만약 Lemma 3을 사용하여 찾은 매칭이 $(1 - 2 \epsilon)\mu$ 이하일 경우 전체 알고리즘을 바로 종료한다.
- MatchingOrCut$(G, k, \mu(1 - 3\epsilon))$ 을 호출하여, $\mu (1 - 4\epsilon)$ 이상의 fractional matching이 있는지를 판별한다. 만약에 존재하지 않는다면, 컷에 속하는 간선 ($e \in S_L \rightarrow R \setminus S_R$) 들 중 $\kappa(e) < 1$ 인 간선들의 가중치를 두 배 증가시키고 다시 반복한다. 이 연산을 doubling 이라고 한다. ($n$ 이 2의 멱승이니 $\kappa(e) \in {1, 0.5, 0.25, \ldots }$ 를 만족함을 상기하자)
- $M$ 을 MatchingOrCut 함수가 반환한 fractional matching으로 정하고 쿼리를 받아들일 준비를 한다.
Algorithm: Edge Deletion $(u, v)$ 를 $G$ 에서 지우고, 지운 간선의 $\kappa(e)$ 값 합을 카운터로 관리한다. 관리된 카운터가 $\mu \epsilon$ 을 넘어갈 경우, 다시 Initialize로 넘어간다.
이상의 내용을 통해서 RobustMatching 알고리즘이 Theorem 1의 요구사항을 구현함은 쉽게 확인할 수 있다. 단지 확인해야 할 것은 이 알고리즘이 정말 $O(m \log^2(n) / \epsilon^3)$ 에 작동하는지 여부이다. 이를 증명하자.
Definition: Min-cost matching potential.
- 각 간선 $e$ 에 대해 $c(e) = \log(\kappa(e) n^2)$ 로 정의하자. $\kappa(e) \geq 1/n^2$ 인 이상 $c(e) \geq 0$임을 확인하자.
- $M_{big}$ 를 크기가 $(1 - \epsilon) \mu(G)$ 이상인 모든 integral 매칭의 집합이라고 하자. $M_{big}$ 은 integral하기 때문에 $\kappa(e)$ 와 아무 상관 없고 용량 제한을 어길 수 있다.
- $\Pi = min_{M \in M_{big}} (\sum_{e \in M} c(e))$ 라고 하자. 즉 $M_{big}$에 있는 큰 integral 매칭 중 $c(e)$ 함수 기준 최소 비용을 뜻한다.
Lemma 4. 알고리즘 종료 전까지 $\Pi = O(\mu \log n)$ 이다.
Proof. 알고리즘이 종료하지 않았으니 최대 정수 매칭이 $(1 - \epsilon) \mu$ 이상이다. 고로 $M_{big}$ 도 공집합이 아니다. 임의의 $M \in M_{big}$ 에 대해 $c(M) \le |M| \log (n^2) = O(\mu \log n)$ 이다. ($\kappa(e) \le 1$ 임을 상기)
Lemma 5. $\Pi \geq 0$ 이며 $\Pi$ 는 감소하지 않는다.
Proof. $c(e) \geq 0$ 이기 때문에 $\Pi \geq 0$ 임은 쉽게 볼 수 있다. 알고리즘 실행 과정에서 $c(e)$ 는 증가하거나, 간선이 사라진다. 두 연산 모두 $\Pi$ 를 감소시킬 수 없다.
Lemma 6. Initialize 알고리즘이 간선의 가중치를 두배 증가시키는 과정을 진행하면, $\Pi$ 가 최소 $\epsilon \mu$ 이상 증가한다.
Proof. $M_{big}$ 에 속하는 임의의 매칭 $M$ 을 고르자. MatchingOrCut 함수가 반환한 컷 간선 집합 $C$ 에서, $\kappa(e) < 1$ 인 간선들의 집합을 $C_{<1}$ 이라고 하자. 반대로, $\kappa(e) = 1$ 인 간선들의 집합은 $C_{=1}$ 이라고 하자. 이 때 $C$ 에 들어간 간선들은 원래 그래프의 간선이 아니라, source/sink를 잇는 간선 역시 포함함을 상기하라. 핵심은, $|M \cap C_{<1}| \geq 2\epsilon \mu$ 임을 증명하는 것이다.
- 첫 번째로, $|M \setminus C_{<1} | \le |C_{=1}|$ 임을 보인다. $M \setminus C_{<1}$ 인 간선들은 $M \cap C_{=1}$ 에 속하거나, 아니면 양 끝점이 컷의 같은 사이드에 속한다. 전자의 경우는 $C_{=1}$ 의 원래 그래프 간선 부분에 속한다고 볼 수 있다. 후자의 경우 일반성을 잃지 않고 매칭 간선이 source 쪽에 연결되어 있다고 하자. 이 간선과 sink를 잇는 간선은 $C_{=1}$ 에 속한다. 이러한 식으로, 이들을 모두 $C_{=1}$에 속하는 간선들로 대체하자. 매칭에 속하는 간선이기 때문에, 대체한 간선들은 서로 다르며, 모두 원래 그래프 간선에 속하지 않는다. 고로 위 사실의 증명이 종료된다.
- 두 번째로, $|C_{=1}| \le (1 - 3\epsilon) \mu$ 를 만족한다. 알고리즘에 의해, 찾은 컷의 크기가 $(1 - 3\epsilon)$ 이하이며, 이러한 컷에 가중치 1의 간선이 해당 값보다 많을 수 없기 때문이다.
- 세 번째로, $|M| \geq (1 - \epsilon) \mu$ 를 만족한다.
- 내용을 종합하면 $|M \cap C_{<1}| = |M| - |M \setminus C_{<1}| \geq (1 - \epsilon) \mu - (1 - 3\epsilon) \mu \geq 2\epsilon \mu$ 이다.
$|M \cap C_{<1}|$ 에 속한 간선들은 $c(e)$ 가 정확히 1씩 증가할 것이기 때문에, 임의의 매칭에 대해서 값이 최소 $2 \epsilon \mu$ 씩 증가함을 볼 수 있다.
Lemma 6이 이 챕터의 가장 어려운 부분이고, 이후 자연스럽게 따라갈 수 있다.
Lemma 7. 알고리즘은 doubling 연산을 최대 $O(\log(n) / \epsilon)$ 번 호출한다.
Proof. Lemma 6에 의하여 $\Pi$ 는 항상 $2\epsilon \mu$ 이상 증가한다. 하지만 $\Pi$ 는 최대 $O(\mu \log(n))$ 만큼 증가할 수 있기 때문에, 증가 횟수는 $O(\log(n) / \epsilon)$ 번 이하로 정해진다.
Lemma 8. 알고리즘은 Initialize 함수를 최대 $O(\log(n) / \epsilon^2)$ 번 호출한다.
Proof. $\kappa_{ALL}$ 을 지금까지 삭제된 모든 간선의 가중치 합이라고 하자. 정확히는, 간선 $e$를 삭제하기 직전에 $\kappa_{ALL}$ 에 $\kappa(e)$ 를 더해준다. 우리는 $\kappa_{ALL} \le m / n^2 + $(doubling 연산 수행 횟수)$ \times (1 - 3\epsilon) \mu = O(\mu \log (n) / \epsilon)$ 이며, $\kappa_{ALL}$ 은 항상 증가하고, Preprocess 함수가 호출한 단 한 번 제외, Initialize 호출은 $\epsilon \mu$ 만큼 $\kappa(e)$ 가 증가했을 때만 호출됨을 알고 있다. 고로 $\kappa_{ALL} / (\epsilon \mu)$ 번 이하로만 호출될 수 있으며, 이는 $O(\mu \log(n) / \epsilon^2)$ 이다.
Proof of Theorem 1. 먼저 알고리즘의 정당성은, 알고리즘이 항상 종료하며, 종료하는 시점에 항상 $\mu(1 - \epsilon)$ 초과의 최대 매칭이 없고, 관리되는 매칭이 항상 $\mu (1-3\epsilon)(1-\epsilon) - \epsilon \mu \geq \mu (1 - 5\epsilon)$ 이상이라는 것으로 확인할 수 있다.
알고리즘의 시간 복잡도는, MatchingOrCut 함수의 시간 복잡도, 그리고 해당 함수의 호출 수에 좌우된다. Theorem 2에 의해 MatchingOrCut 함수의 시간 복잡도는 $O(m \log (n) / \epsilon)$ 이다. 호출 수는 Doubling 연산의 수와, Initialize 함수의 호출 수의 합이다. 이는 Lemma 7, 8에 의해 $O(\log(n) / \epsilon^2)$ 이다. 고로 총 시간 복잡도는 $O(m \log^2(n) / \epsilon^3)$ 이다.
Theorem 2의 증명: Bounded-height push-relabel을 사용한 MatchingOrCut 알고리즘
이제 다음과 같은 내용의 Theorem 2를 증명할 일만 남았다.
Theorem 2. Matching-Or-Cut 알고리즘은 $G = (L \cup R, E)$ 과 용량 함수 $\kappa : E \rightarrow R_{(0, 1]}, \mu \in [1, n], \epsilon \in (0, 1)$ 을 입력으로 받아 $O(m \log(n) / \epsilon)$ 시간에 둘 중 하나를 반환한다.
- $val(e) \le \kappa(e)$ 를 만족하는 크기 $\mu(1 - \epsilon)$ 의 fractional matching $M$
- $\kappa(S_L, R \setminus S_R) + |S_R| \le \mu + |S_L| - n$ 을 만족하는 두 집합 $S_L \subseteq L, S_R \subseteq R$
이를 위해서 우리는 Bounded Height Push-relabel이라는 것을 사용한다. 만약 Push-relabel 알고리즘에 대한 지식이 없다면, 이전 작성한 글 에서 배우고 돌아오자.
Notation summary
Flow 노테이션은 저자에 따라 항상 다르기 때문에 여기서도 이전에 작성한 글과 조금 다른 노테이션을 사용한다.
- Source와 Sink 정점을 따로 두는 대신, 함수 $\Delta : V \rightarrow R_{\geq 0}$ 과 $T : V \rightarrow R_{\geq 0}$ 을 둔다. 이는 정점 $v$ 로 Source에서 $\Delta(v)$ 만큼의 용량을 가진 간선이, 정점 $v$ 에서 Sink 방향으로 $T(v)$ 만큼의 용량을 가진 간선이 존재함을 뜻한다.
- 항상, Source에서 나온 supply를 전부 흘려야 한다고 생각한다. 즉, Source에서는 항상 정확히 $\Delta(v)$ 만큼의 용량이 각 정점으로 가야 한다.
고로, 플로우 문제는 입력으로 그래프 $G = (V, E)$ 및 함수 $\Delta, T$ 그리고 용량 $c : E \rightarrow R_{\geq 0}$ 을 받는다.
이렇게 노테이션을 두었을 때, Excess라는 개념을 조금 더 자연스럽게 정의할 수 있다. 각 간선의 유량을 $f(u, v)$ 라고 하면, $\Delta(v) + \sum_u f(u, v) \le T(v)$ 가 성립하기만 하면 Valid flow라고 생각할 수 있다. 만약에 항이 음수가 되면 Source에서 유량을 빌려오고, 양수가 되면 Sink로 유량을 보내주면 되기 때문이다. 고로, Valid한 flow는 Edge capacity, antisymmetry 조건을 만족하면서 위 부등식을 만족해야 한다. 편의상 $f(v) = \Delta(v) + \sum_u f(u, v) $ 라고 한다.
Valid한 flow를 정의하였으니 preflow 역시 정의할 수 있다. Preflow는 $f(v) \le T(v)$ 조건이 성립하지 않을 수 있는 플로우 $f$ 를 뜻한다. 원래 사용하던 개념의 excess 는 여기서 $max(0, f(v) - T(v))$ 에 대응된다고 볼 수 있다. 이 값을 $ex(v)$ 라고 하고, 또한 $ab(v) = min(f(v), T(v)) = f(v) - ex(v)$ 를 $v$ 가 흡수한 플로우 양이라고 정의하자.
Bounded height push-relabel
Proposition 2.1. 방향성 있는 그래프 $G = (V, E)$, 함수 $(\Delta, T, c)$, 그리고 높이 파라미터 $h \geq 1$가 주어졌을 때, preflow $f$ 와, 라벨 함수 $l : V \rightarrow {0, \ldots, h}$ 를 반환하는 다음과 같은 알고리즘이 존재하며, 이 알고리즘은 $O(mh \log m)$ 에 동작한다.
- $l(u) > l(v) + 1$ 이며 $(u, v) \in E$ 일 경우 $(u, v)$ 는 포화 간선이고, $(v, u)$ 를 흐르는 유량은 없다.
- $l(v) < h$ 일 경우 $ex_f(v) = 0$ 이다.
- $l(v) > 0$ 일 경우 $ab_f(v) = T(v)$ 이다.
Proposition 2.1의 명세는 Push-relabel의 그것과 아주 유사하다. 차이점은, 라벨 함수가 가질 수 있는 값의 범위가 $|V|$ 보다 작은 $h$ 라는 값일 수 있다는 것이다. 하지만 신기하게도 이것을 Push-relabel을 사용하여 구하지는 않는다.
Proof. 일반적인 정의에서 하던 대로, 소스와 싱크에 대응되는 정점 $s, t$ 를 만들어 준 후, Blocking Flow를 $h+2$ 번 찾아준다. Blocking flow는 플로우가 fractional하더라도, link-cut tree를 사용하여 $O(m \log m)$에 구해줄 수 있다. Blocking flow를 구한 이후, Residual graph에서 소스와 싱크 사이의 거리는 최소 $h + 2$ 이상이다. $l(v) = max(0, h + 1 - dist(s, v))$ 라고 두자. 그렇다면
- 만약 $l(u) > l(v) + 1$ 인데 Residual graph에서 $(u, v)$를 잇는 간선이 존재한다면, $dist(s, u) + 1 < dist(s, v)$ 라는 뜻이기 때문에 가정에 모순이다.
- 소스와 싱크를 지워주고 다시 preflow로 전환하였을 경우, 각 정점이 흡수한 플로우 양은 $ab(v) = f(v, t)$ 이고, Excess는 $\Delta(v)$ 만큼의 유량 중 흘리지 못한, 즉 $\Delta(v) - f(s, v)$ 이다. $ex_f(v) > 0$ 이라면 source에서 $v$ 로 가는 residual edge가 있으니 $l(v) = h$ 이다. $ab(v) < T(v)$ 라면 $v$ 에서 sink로 가는 residual edge가 있으니 $l(v) = 0$ 이다.
여담으로, 이를 통해서 Push-relabel과 Blocking flow가 사실은 완전히 동일한 것을 하는 알고리즘이라는 직관을 얻을 수 있다. (정확히는, 이 level 이라는 것이 Flow LP의 Dual과 같은 역할을 하는 것이다. 느낌만 있고, 정확한 statement로 적을 수 있는지는 모르겠다. 좋은 고견이 있다면 토론해 보면 좋을 것 같다.)
편의상 다음과 같은 Notation을 사용한다.
Definition 2.2 정점에 대한 라벨 함수 $l : V \rightarrow {0, \ldots, h}$ 가 주어질 때, $V_i = {u | l(u) = i}$ 로 정의한다. $V_{\geq i} = {u | l(u) \geq i}$ 로 정의하며, $V_{>i}, V_{\leq i}, V_{< i}$등도 비슷하게 정의된다.
우리가 다루는 그래프는 $V = L \cup R$ 형태의 이분 그래프며, source에서 $L$ 로 가는 간선, $R$ 에서 sink로 가는 간선으로 이루어져 있다. 이 경우 다음과 같은 성질이 성립한다.
Lemma 2.3 $V = L \cup R$ 형태의 이분 그래프에서, 모든 $v \in R$ 에 대해 $\Delta(v) = 0$이고, $v \in L$ 에 대해 $T(v) = 0$ 이라면, Proposition 2.1에서 구한 라벨링에 대해 $V_{h}, V_{h-2}, V_{h-4}, \ldots \subseteq L$, $V_{h-1}, V_{h-3}, V_{h-5}, \ldots \subseteq R$ 이 성립한다. (증명은 Blocking flow 알고리즘의 성질에 따라 자명하다)
MatchingOrCut 알고리즘은 excess 가 작은 (즉, 충분히 큰) 플로우를 찾지 못할 경우 크기가 작은 컷을 반환해야 한다. 우리가 찾을 컷의 후보는 레벨에 따른 컷, 즉 $(V_{\geq i}, V_{<i})$ 의 형태이다. ($i \in [h]$) 아래 소개할 Lemma들은 이러한 목표를 위해 설계되었다. 먼저 첫 번째 Lemma는, $V_h, V_0$ 의 크기가 충분히 크다는 것을 보이기 위한 장치이다.
Lemma 2.4 $\Delta(V) \le T(V)$ 인 경우, $\Delta(V_h) \geq ex_f(V)$ 이며 $T(V_0) \geq ex_f(V)$ 이다.
Proof. Prop 2.1에 의해 $ex_f(V_{<h}) = 0$ 이며, $v \in V_h$ 에 대해 $ex_f(v) = \Delta(v) - f(s, v) \le Delta(v)$ 이다. 또한, $T(V) \geq T(V) - ab_f(V) \geq \Delta(V) - ab_f(V) \geq ex_f(V)$ 이다.
다음 Lemma는 우리가 찾을 컷 후보 $(V_{\geq i}, V_{<i})$ 의 용량 합이 작다는 것을 보이기 위한 장치이다.
Lemma 2.5 $c(E(V_{\geq i}, V_{<i}) \setminus E(V_i, V_{i-1})) \leq \Delta(V_{\geq i}) + f(V_{i-1}, V_i) - ab_f(V_{\geq i}) - ex_f(V_{\geq i})$
Proof. 먼저, 좌변에 있는 간선 $(u, v)$ 에 대해서 $l(u) - l(v) > 1$ 이 성립한다. 고로 이 간선들은 Prop 2.1에 의해 $f(u, v) = c(u, v)$ 가 성립한다. 결론적으로, 좌변은 $V_{\geq i}$ 에서 나가는 유량의 일부이기 때문에, $V_{\geq i}$ 에서 나가는 총 유량보다 작거나 같다. 우변의 식이 정확히 $V_{\geq i}$ 에서 나가는 총 유량이다. $V_{\geq i}$ 에서 나가는 유량은, (source로 들어온 유량) + ($(V_{<i}, V_{\geq i})$ 로 들어온 유량) - (sink로 나간 유량) - (excess) 가 될 것이다. $(V_{<i}, V_{\geq i})$ 로 들어온 유량은, $(V_{i-1}, V_{i})$ 에서만 0 초과일 수 있다. 그 외의 경우 Prop 2.1에 의해서 0이기 때문이다. 고로 우변의 식은 정확히 $V_{\geq i}$ 로 들어온 유량 합이다.
이제 Theorem 2를 증명하기 위한 마지막 Lemma를 소개할 준비가 되었다.
Lemma 2.6 (Global Flow For Matchings). 방향성 있는 이분 그래프 $G = (L \cup R, E)$ 와, Excess parameter $z \geq 0$, height parameter $h \geq 1$, 플로우 문제 $(\Delta, T, c)$ 가 주어진다. 추가로 플로우 문제는 다음과 같은 성질을 만족한다:
- $\Delta(R) = 0, T(L) = 0, \Delta(L) \leq T(R)$
- 모든 $v \in V$ 에 대해 $\Delta(v), T(v) \leq 1$
이 때 $O(mh \log m)$ 시간에, 알고리즘은
- 총 Excess가 $ex_f(L \cup R) \leq z$ 인 preflow $f$ 를 반환하거나
- $|S|, |V \setminus S| > z$ 이며 $c(E(S, V \setminus S)) \leq \Delta(S) - T(S) - z + 2\frac{\Delta(V) - z}{h}$ 인 집합 $S \subset V(G)$ 를 반환한다.
Proof. Proposition 2.1을 $O(mh \log m)$ 시간에 걸쳐 수행한다. 만약 $ex_f(V) \leq z$ 일 경우 그대로 preflow를 반환한다. 고로 $ex_f(V) > z$ 라고 하자. Lemma 2.4에 의해 $\Delta(V_h) > z, T(V_0) > z$ 이다. 한편 $\Delta(v), T(v) \leq 1$ 이기 때문에 이는 $|V_h| > z, |V_0| > z$ 임을 뜻한다. Lemma 2.3에 의해서 $V_h, V_{h - 2}, \ldots \subseteq L, V_{h-1}, V_{h-3}, \ldots \subseteq R$ 을 만족한다. 고로 $\sum_{i > 0} f(V_{h - 2i}, V_{h-2i+1}) \leq f(L, R)$ 이다. $L$ 로 들어온 supply는 $L$ 에서 absorb되지 않고, $R$ 로 나가거나 excess로 쌓이기 때문에, $f(L, R) \leq \Delta(V) - z$ 이다. 즉, $f(V_{h-2i}, V_{h-2i+1}) \le 2(\Delta(V) - z) / h$ 인 $1 \le i \le h/2$ 가 존재한다.
이러한 $i$ 를 고정하고, $S = V_{> h - 2i}$ 라 두자. $V_h \subseteq S, V_0 \subseteq V\setminus S$ 이니 $|S|, |V \setminus S| > z$ 이다. 이 컷의 크기를 산출해 보면
$c(E(S, V\setminus S)) = c(E(V_{h-2i+1}, V_{h- 2i})) + c(E(V_{>h-2i}, V_{\le h-2i}) \setminus E(V_{h-2i+1}, V_{h-2i}))$
그런데 $R \rightarrow L$ 로 가는 간선이 없으니 우변의 첫 번째 항은 $0$ 이다. 두 번째 항은 Lemma 2.5에 의해
$c(E(S, V\setminus S)) \le \Delta(V_{>h-2i}) + f(V_{h-2i}, V_{h-2i+1}) - ab_f(V_{>h-2i}) - ex_f(V_{>h-2i})$
$c(E(S, V\setminus S)) \le \Delta(S) + 2(\Delta(V) - z) / h - ab_f(S) - ex_f(S)$
$ab_f(S) = T(S)$, $ex_f(S) = ex_f(V) > z$ 이니
$c(E(S, V\setminus S)) \le \Delta(S) - T(S) - z + 2(\Delta(V) - z) / h$ 이다. $\blacksquare$
모든 준비가 끝났고, 글을 마무리하는 마지막 Theorem을 도입할 차례이다.
Theorem 2. Matching-Or-Cut 알고리즘은 $G = (L \cup R, E)$ 과 용량 함수 $\kappa : E \rightarrow R_{(0, 1]}, \mu \in [1, n], \epsilon \in (0, 1)$ 을 입력으로 받아 $O(m \log(n) / \epsilon)$ 시간에 둘 중 하나를 반환한다.
- $val(e) \le \kappa(e)$ 를 만족하는 크기 $\mu(1 - \epsilon)$ 의 fractional matching $M$
- $\kappa(S_L, R \setminus S_R) + |S_R| \le \mu + |S_L| - n$ 을 만족하는 두 집합 $S_L \subseteq L, S_R \subseteq R$
Proof of Theorem 2. 일반성을 잃지 않고 $|L| \leq |R|$ 이라고 하자. 플로우 모델링과 유사하게 각 간선을 $L \rightarrow R$ 로 가는 방향 간선으로 생각한다. $h = 2/\epsilon, z = n - \mu(1 - \epsilon)$ 이라고 둔다. $v \in L$ 에 대해서 $\Delta(v) = 1$, $v \in R$ 에 대해서 $T(v) = 1$ 이다. $c = \kappa$ 이다. 이제 Lemma 2.6의 알고리즘을 호출하자. 모든 Argument가 Lemma 2.6의 조건을 만족하며, 알고리즘이 $O(m \log m / \epsilon)$ 시간에 종료함을 볼 수 있다.
만약 Lemma 2.6의 알고리즘이 excess가 $z$ 이하인 preflow $f$ 를 반환하면, 이는 $\Delta(v) - z = \mu (1 - \epsilon)$ 이상의 매칭이니 좋다. (정확히는, 단순히 excess를 그냥 제거해줘도 valid flow $f$ 가 나온다.) 그렇지 않다면, $\kappa(E(S, V\setminus S)) \le \Delta(S) - T(S) - z + 2(\Delta(V) - z) / h$인 집합을 찾을 수 있다. $S_L = S \cap L, S_R = S \cap R$ 이라고 하자. $\kappa(S_L, R \setminus S_R) \le |S_L| - |S_R| - (n - \mu(1 - \epsilon)) + 2(\mu(1 - \epsilon))/(2/\epsilon) \le |S_L| - |S_R| - n + \mu(1 - \epsilon)(1 + \epsilon) \le |S_L| - |S_R| - n + \mu$. $\blacksquare$
참고 자료
'공부 > CS theory' 카테고리의 다른 글
| Inapproximability in computational hardness (0) | 2022.11.01 |
|---|---|
| Shortest Cycle Through Specified Elements (0) | 2022.06.07 |
| Efficient Primal-Dual Algorithms for MapReduce (0) | 2022.01.08 |
| Constructing a Distance Sensitivity Oracle in O(n^{2.5794}M) Time (0) | 2021.10.10 |
| Incremental Topological Ordering and Strong Component Maintenance (0) | 2021.06.27 |
- Total
- Today
- Yesterday
