티스토리 뷰
Constructing a Distance Sensitivity Oracle in O(n^{2.5794}M) Time
구사과 2021. 10. 10. 23:25가중치 있는 방향 그래프 $G$ 에서 두 정점 $s, t$ 가 쿼리로 주어질 때, $s$ 에서 $t$ 로 가는 최단 경로를 구하는 문제를 흔히 모든 쌍 최단 경로 문제 (All-Pair Shortest Path, APSP) 문제라고 부른다. APSP 문제는 그래프 이론의 기초적인 문제 중 하나로, Floyd-Warshall Algorithm을 사용하여 $O(n^3)$ 시간에 해결하는 방법이 아주 잘 알려져 있으며 알고리즘을 공부하다 보면 누구나 접하게 될 기초 알고리즘 중 하나이다.
Floyd Warshall Algorithm은 APSP 문제에 대해서 다음과 같은 자료구조를 만드는 알고리즘이라고 볼 수 있다:
- 자료 구조의 초기화에는 $O(n^3)$ 이 걸린다.
- 자료 구조는 $O(n^2)$ 의 메모리를 사용한다.
- 자료 구조는 각 쿼리를 $O(1)$에 처리한다.
여기서 Floyd-Warshall Algorithm을 Dijkstra로 대체할 경우 초기화 시간을 $\tilde{O}(mn)$ 으로 최적화 할 수 있다. 많은 전문가들은 APSP는 이보다 더 빠르게 해결할 수 없다고 믿는다 (APSP Conjecture).
Distance-Sensitivity Oracle (DSO)는 APSP 문제를 일반화하는 문제로, 각 쿼리에서 두 정점 $s, t$ 와 실패 위치 $f$가 주어진다. 실패 위치는 하나의 간선이나 하나의 정점이다. 쿼리가 주어지면, 우리는 $s$ 에서 $t$ 로 가며 $f$를 지나지 않는 최단 경로를 찾아야 한다. 단순하게는, APSP 알고리즘을 모든 $f$ 에 대해서 수행함으로써 $O(n^3m)$ 시간에 $O(n^2m)$ 메모리를 사용하는 자료구조를 만들 수 있다. 일반 그래프에 대해서는 이 문제에 대한 많은 연구가 이루어져 있으며, 2017년 기준 $\tilde{O}(nm)$ 시간과 $O(n^2)$ 메모리로 DSO 문제를 해결할 수 있다. 이는 이 문제의 하위호환인 APSP와 동일한 시간/메모리 를 사용하며, APSP Conjecture에 의해 APSP를 이보다 더 빠르게 풀 수 없다면, DSO 역시 이보다 더 빠르게 해결할 수는 없을 것이다.
하지만, 간선의 가중치가 $[-M, M]$ 이며 그래프가 Dense하다면 ($m = \Theta(n^2)$), APSP를 더 빠르게 해결할 수 있다는 사실이 잘 알려져 있다. 예를 들어, Undirected graph에서는 APSP를 $\tilde{O}(n^{\omega} M)$ 에 풀 수 있으며, Directed graph에서는 APSP를 $O(n^{2.5286}M)$ 에 해결할 수 있다 (Zwick '02). 이러한 결과로 미루어 봤을 때, DSO에서도 비슷한 방식으로 빠른 알고리즘이 있는지를 자연스럽게 질문할 수 있다. 이에 대한 정답은 (거의) 참으로 밝혀졌으며, Chechik과 Cohen은 $O(n^{2.873}M)$ 시간에 작동하며 각 쿼리를 polylogarithmic time에 처리하는 DSO를 구성하였다.
모든 간선의 가중치가 양수라고 가정하면, Constructing a Distance Sensitivity Oracle in $O(n^{2.5794}M)$ Time 라는 논문은 $O(n^{2.5794}M)$ 시간에 $O(1)$ 쿼리를 지원하는 DSO를 구성할 수 있음을 보인다. 이는 APSP와 $O(n^{0.051})$ 배 차이밖에 나지 않는 결과로, DSO와 APSP의 Gap을 크게 줄이는 결과이다. 이 글에서는 이 논문의 내용을 요약한다.
1. Introduction
이 논문의 Main result는 다음과 같다.
Theorem 1. 간선의 가중치가 ${1, 2, \ldots, M}$ 중 하나인 방향 그래프 $G = (V, E)$ 가 주어지면, $O(n^{2.5794}M)$ 시간에 전처리하고, $O(1)$ 시간에 쿼리를 지원하는 DSO를 구성할 수 있다.
Remark on Theorem 1. 알고리즘의 Exponent에 $\omega$ 가 등장하지 않는 이유는, 이 알고리즘이 정사각형 행렬을 곱하는 것이 아니라 직사각형 행렬을 곱하기 때문이다.
이제 이어지는 내용은 Theorem 1을 증명하기 위해 사용된다.
2. Technical Preliminaries
Main Result를 증명하기 위해서는 $x^r$ Modulo 상에서 Polynomial matrix의 역행렬을 계산해야 한다. $r$ 을 어떠한 정수, $\mathbb{F}$ 를 어떠한 유한 체 (Finite field), $F \in \mathbb{F}[x]^{n \times n}$ 를 각 항이 $d$ 차 다항식인 행렬이라고 하자. 다음 내용이 성립한다.
Theorem 2 (Proof omitted in this article). $F^{-1} \mod x^r$ 를 $\tilde{O}(dn^{\omega}) + (r^2/d) \times MM (n, nd/r, nd/r) \times n^{o(1)}$ 시간에 계산할 수 있다.
이 때 $\omega$ 는 행렬 곱 알고리즘의 지수부 상수이다. 현재 $\omega \le 2.3728596$ 임이 알려져 있다. $MM(n_1, n_2, n_3)$ 은 $n_1 \times n_2$ 행렬과 $n_2 \times n_3$ 행렬을 곱하는 데 걸리는 시간이다. 이 Theorem의 증명이 이 논문에 나와 있지만, 이 글에서는 technical하여 굳이 다루지 않는다.
3. Constructing a $r$-truncated DSO in $O(n^{2.5794}M)$ time
Main Theorem을 증명하기 위해 다음과 같은 조금 더 간단한 문제를 해결한다. 이 부분이 이 논문의 핵심인데, 놀랍게도 상당히 간단한 아이디어로 해결할 수 있다.
쿼리 $(u, v, f)$ 에 대한 최단 경로를 $l$ 이라고 할 때, $l$ 을 반환할 수는 없지만, $min(l, r)$ 을 반환할 수 있는 DSO를 $r$-truncated DSO 라고 정의한다. 이제 이러한 $r$-truncated DSO 를 $\tilde{O}(dn^{\omega}) + (r^2/d) \times MM (n, nd/r, nd/r) \times n^{o(1)} = O(n^{2.5794}M)$ 시간에 계산할 수 있는 알고리즘을 제시한다.
$\mathbb{F}$ 를 충분히 큰 유한체, 예를 들어 $Z_p$ 라고 하고, 그래프 $G$ 에 대해 $A(G)$ 라는 행렬을 다음과 같이 정의하자.
- 만약 $u \rightarrow v$ 로 가는 가중치 $l$ 의 간선이 존재한다면, $A(G){u, v} = a{u, v} x^l$ 이다. 이 때 $a_{u, v}$ 는 $\mathbb{F} \setminus {0}$ 에 속하는 어떤 랜덤 원소이다.
- 모든 $v$ 에 대해서 $A(G)_{v, v} = 1$ 이다.
다음과 같은 사실이 잘 알려져 있다. (최근 카이스트 교내 대회에도 이에 관련된 문제가 출제되었다.)
Lemma 3.1 (Sankowski, 2005). $A(G)$ 의 adjoint matrix를 $adj(A(G))$ 라고 할 때, $adj(A(G))_{u, v}$ 의 최소차항의 차수는 $u$ 에서 $v$ 로 가는 최단 경로의 길이와 높은 확률로 일치한다.
Proof of Lemma 3.1. $P(n)$ 을 길이 $n$ 의 모든 수열의 집합이라 하면, 정의에 의해 $adj(A(G))_{u, v} = \sum_{p \in P(n), p_v = u} \prod_{k \in [n] \setminus \{v\}} A(G)_{k, p_k}$ 이다. 그래프 이론적으로 해석했을 때, 이것은 모든 정점들을 사이클과 $u \rightarrow v$ 로 가는 경로로 분해하고, 분해에 사용된 간선의 가중치 합을 곱한 것이다. 만약 최단 경로가 $u \rightarrow v$ 를 잇는 사이클로 분해되고, 최단 경로에 속하지 않는 정점들에 대해 Self-loop로 분해한다면, 최소 차항이 $dist(u, v)$ 인 항을 하나 얻을 수 있다. 고로 $adj(A(G))_{u, v}$ 의 $dist(u, v)$ 차항은 높은 확률로 0이 아니다. 역으로, $adj(A(G))_{u, v}$ 에 어떤 0이 아닌 $k$ 차항이 존재한다고 하자. 사이클에 있는 간선들을 모두 지워주면 $u \rightarrow v$ 로 가는 길이 $k$ 이하의 경로를 얻을 수 있다. 종합하면, $adj(A(G))_{u, v}$ 의 최소 차항과 $dist(u, v)$ 는 일치한다는 결론을 얻는다. $\blacksquare$
다음과 같은 사실은 훨씬 더 잘 알려져 있다.
Theorem 3.2 (Sherman-Morrison-Woodbury Formula) Field $\mathbb{F}$, Invertible matrix $A \in \mathbb{F}^{n \times n}$, Column vector $u, v \in \mathbb{F}^n$ 에 대해서, $\gamma = 1 + v^T A^{-1} u$ 라고 하자. $\gamma$ 가 Invertible하다면 $A + uv^T$ 역시 invertible하고,
- $det(A + uv^T) = \gamma det(A)$
- $(A + uv^T)^{-1} = A^{-1} - \gamma^{-1} (A^{-1} u v^T A^{-1})$
- $adj(A + uv^T) = det(A + uv^T) (A + uv^T)^{-1} = det(A) (\gamma A^{-1} - A^{-1} uv^T A^{-1})$
또한 Schwartz-Zippel Lemma를 사용한다.
Theorem 3.3 (Schwartz-Zippel Lemma) Field $\mathbb{F}$ 에서 $p(x_1, x_2, \ldots, x_m)$ 을 총 차수가 $d$ 이하인 0이 아닌 다항식이라고 하자. $S$ 를 $\mathbb{F}$ 의 유한한 부분집합이라 하고, $r_1, r_2, \ldots, r_m$ 을 $S$ 에서 independently, uniformly sampled한 변수라고 할 때, $Pr[p(r_1, r_2, \ldots, r_m) = 0] \le \frac{d}{|S|}$ 이다.
$F \in \mathbb{F}[x]^{n \times n}$ 를 각 항이 $d$ 차 다항식인 행렬이라고 하자. 다음 내용이 성립한다.
Theorem 3.4. $det(F)$ 를 $\tilde{O}(dn^\omega)$ 번의 field operation으로 계산할 수 있다.
이를 Theorem 2와 결합하면
Corollary 3.5. $adj(F) \mod x^r$ 을 $\tilde{O}(dn^{\omega}) + (r^2/d) \times MM (n, nd/r, nd/r) \times n^{o(1)}$ 시간에 계산할 수 있다.
이제 알고리즘에 대한 설명을 할 준비가 완료되었다.
3.1 Preprocessing Algorithm
전처리 알고리즘은 아주 간단하다. 충분히 큰 상수 $C$ 에 대해서 단순히 $p \in [n^C, 2n^C]$ 를 구하고, $\mathbb{F} = \mathbb{Z}_p$ 로 둔다. 그리고 위에서 설명한 것과 같이 $A(G)$ 를 만들고, Theorem 2, Theorem 3.4 에 의해 $A(G)^{-1}, det(A(G))$ 를 구한다. 이것으로 전처리 알고리즘이 종료된다.
3.2 Query Algorithm
쿼리 알고리즘 역시 간단한 편이다. Theorem 3.2에 설명된 Sherman-Morrisson-Woodbury를 사용하면, 간선이나 정점을 지운 후의 Adjoint matrix를 쉽게 계산할 수 있다. 위 수식을 그대로 사용할 경우 $O(n^2)$ 시간에 새로운 Adjoint matrix를 구할 수 있고 이것만으로도 이미 Naive algorithm보다 효율적이다. Theorem 3.2의 역행렬이 누적되는 형태가 아니며, 각 쿼리에서 우리가 원하는 것은 전체 Adjoint matrix가 아니라 항 하나이기 때문에, 이 점을 활용하면 굳이 행렬을 계산할 필요 없이 항 하나를 $O(1)$ 번의 Arithmetic operation으로 구할 수 있다. 이것이 사실상 쿼리 알고리즘의 전부이지만, 완결성을 위해서 정확한 수식을 아래 첨부한다. 특별히 필요하지 않으면 웬만하면 여기서 3.3으로 넘기는 것을 추천한다.
3.2.1 Query Algorithm for Edge Failure
$e = (i \rightarrow j)$ 가 삭제되고, $x$ 에서 $y$ 로 가는 최단 경로를 계산한다고 하자. $A(G)_{i, j}$ 에 $-a_{i, j}x^{w(i, j)}$ 을 더해야 한다. 이는 $u = e_i, v = -a_{i, j}x^{w(i, j)} e_j$ 일 때 $A^\prime(G) = A(G) + uv^T$ 를 설정하는 것과 같다. Theorem 3.2를 적용시킬 준비를 하자.
- $\gamma = 1 + v^T A(G)^{-1} u$
- $\beta = (A(G)^{-1} uv^T A(G)^{-1})_{x, y}$
이 항들은 모두 $O(1)$ 시간에 계산 가능하다:
- $\gamma = 1 + v^T A(G)^{-1} u = 1 - a_{i, j} x^{w(i, j)} A(G)^{-1}_{j, i}$
- $\beta = (A(G)^{-1} uv^T A(G)^{-1})_{x, y} = -A(G)^{-1}_{x, i} z_{i, j} A(G)^{-1}_{j, y} x^{w(i, j)}$
이제 $A^\prime(G)_{x, y} = det(A(G)) (\gamma A(G)^{-1}_{x, y} - \beta)$ 이니 $O(1)$ 번의 arithmetic operation으로 쿼리의 정답을 계산할 수 있다.
3.2.2 Query Algorithm for Vertex Failure
정점 $f$ 가 삭제되고, $u$ 에서 $v$ 로 가는 최단 경로를 계산한다고 하자. 일반성을 잃지 않고 $f \neq u, f \neq v$ 를 가정할 수 있다. $f$ 에서 나가는 모든 간선을 제거하는 것으로 충분하며, 이는 Row vector 하나를 $f$ 행에 더하는 rank-1 update이니 Theorem 3.2를 적용할 수 있다. $u = e_f$, $v$ 를 $A(G)^T$ 의 $f$번째 행의 역 (negation) 에서 $v_f = 0$ 을 취한 벡터라고 하자. 다시 말해
$\begin{equation}
v_j =
\begin{cases}
-a_{f, j} x^{w(f, j)}, & \text{if $f \neq j$}.\newline
0 & \text{otherwise}.
\end{cases}
\end{equation}$
이제 $A^\prime(G) = A(G) + uv^T$ 이다. Theorem 3.2를 적용시킬 준비를 하자.
- $\gamma = 1 + v^T A(G)^{-1} u$
- $\beta = (A(G)^{-1} uv^T A(G)^{-1})_{x, y}$
이 항들은 모두 $O(1)$ 시간에 계산 가능하다:
- $(e_f - v)^T$ 는 정확히 $A(G)$ 의 $f$ 번째 행이다. $(e_f - v)^T A(G)^{-1} = e_f^T$. $v^T A(G)^{-1} = e_f^T A(G)^{-1} - e_f^T$ . 고로 $\gamma = 1 + e_f^T A(G)^{-1} u - e_f^T u = A(G)^{-1}_{f, f}$
- $\beta = (A(G)^{-1} uv^T A(G)^{-1})_{x, y} = (e_u^T A(G)^{-1}u) (v^T A(G)^{-1} e_v) = A(G)^{-1}_{u, f} A(G)^{-1}_{f, v}$
이제 $A^\prime(G)_{x, y} = det(A(G)) (\gamma A(G)^{-1}_{x, y} - \beta)$ 이니 $O(1)$ 번의 arithmetic operation으로 쿼리의 정답을 계산할 수 있다.
이를 종합하여 우리는 다음과 같은 결론을 얻는다.
Theorem 3.6. 간선의 가중치가 ${1, 2, \ldots, M}$ 중 하나인 방향 그래프 $G = (V, E)$ 가 주어지면, $O(n^{2.5794}M)$ 시간에 전처리하고, $O(1)$ 시간에 쿼리를 지원하는 $r$-truncated DSO를 구성할 수 있다.
Proof of Theorem 3.6. 알고리즘의 정당성은 자명하다. 확률 분석을 해 보면, 쿼리 알고리즘이 실패할 가능성이 Theorem 3.3에 의해 $\frac{d}{|S|}$ 이하이다. Determinant는 $n$ 차 다항식이니, 대략 $O(n/n^{C}) = O(1/n^{C - 1})$ 의 확률로 실패한다는 것이다. 가능한 쿼리의 가짓수가 $O(n^4)$ 가지이니, 알고리즘은 $O(1/n^{C - 5})$ 의 확률로 틀린다. 이는 알고리즘이 높은 확률로 (w.h.p) 정답을 반환함을 뜻한다. $\blacksquare$
3.3 Constructing the Full DSO
Theorem 3.6을 통해서 $r$-truncated DSO를 만들었다. 이제 이 $r$-truncated DSO를 Black box로 사용하여 Full DSO를 구성한다.
첫 번째 알고리즘은, 쿼리 타임이 클 수 있는 $r$-truncated DSO를 받아, $O(1)$ 쿼리를 지원하게끔 하는 것이다. 이를 구체적으로 설명하면 다음과 같다.
Lemma 3.7 (Proof omitted in this article) 정수 $r$, 모든 간선의 가중치가 ${1, 2, \ldots, M}$ 인 그래프 $G = (V, E)$, 전처리 시간 $P$ 이며 쿼리 시간 $Q$ 인 임의의 $r$-truncated DSO $D$ 에 대해서, $O(1)$ 쿼리 시간과 $O(n^{2.5286}M + P + \tilde{O}(n^2)Q)$ 전처리 시간을 가지는 $r$-truncated DSO $Fast(D)$ 를 만들 수 있다.
Short explanation. $G$ 의 모든 쌍 최단 경로 행렬과, consistent 한 shortest path tree를 빠르게 구성한 후, $\tilde{O}(n^2)$ 번의 쿼리만으로 모든 중요한 정보를 표현할 수 있다는 것이 이 Lemma의 대략적인 증명이다. Lemma 자체는 Ren20의 Observation 4에서도 사용하였지만, 당시에는 $\tilde{O}(Mn^2)$ 였던 쿼리 횟수를 줄였다는 것이 이 논문의 기여 중 하나이다. 그 내용이 생각보다 길고 복잡해서, 지면 상 문제로 증명은 생략한다.
두 번째 알고리즘은, $O(1)$ 쿼리를 지원하는 $r$-truncated DSO를 받아, 쿼리 타임이 조금 큰 $(3/2)r$-truncated DSO를 만드는 것이다. 이를 구체적으로 설명하면 다음과 같다.
Lemma 3.8. 전처리 시간 $P$ 이며 쿼리 시간 $O(1)$ 인 임의의 $r$-truncated DSO $D$ 에 대해서, $\tilde{O}(nM/r)$ 쿼리 시간과 $P + O(n^2)$ 전처리 시간을 가지는 $r$-truncated DSO $Extend(D)$ 를 만들 수 있다. 이 DSO는 높은 확률로 올바르다.
Proof of Lemma 3.8. $apath(u, v, x)$ 를 $u \rightarrow v$ 로 가는 경로 중 $x$ 를 거치지 않는 최단 경로라고 하자. 모든 $u, v, x$ 에 대해, $P$ 를 $r \le |apath(u, v, x)| < (3/2)r$ 를 만족하는 $apath(u, v, x)$ 들의 집합이라고 하자. $P$ 는 $D$ 에서는 계산할 수 없지만 $Extend(D)$ 에서 계산해야 하는 집합과 정확히 일치한다.
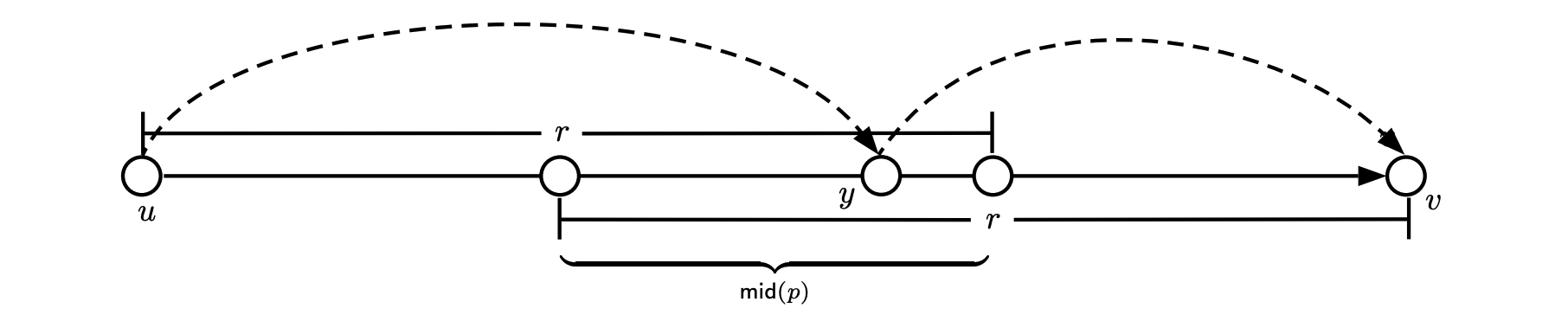
$P$ 의 원소 $p = apath(u, v, x) \in P$ 에 대해, $mid(p)$를 $|p[u, y]| < r, |p[y, v]| < r$ 을 만족하는 정점 $y \in p$ 의 집합이라고 하자. 여기서, $p[a, b]$ 는 경로 $p$ 에서 정점 $a \rightarrow b$ 로 가는 부분경로 (subpath) 이다. 자세한 것은 아래 사진을 참조하라.
$p[u, y] = apath(u, y, x), p[y, v] = apath(y, v, x)$ 이기 때문에, $D$ 에서는 는 $apath(u, y, x), apath(y, v, x)$ 를 올바르게 찾을 수 있다. 즉, 우리가 $y$ 를 찾으면, $apath(u, v, x)$ 역시 찾을 수 있다. 또한, $|mid(p)| \geq r/3M$ 이다.
$Extend(D)$ 의 전처리 알고리즘을 설명한다. 충분히 큰 상수 $C$ 를 고정하자. 모든 정점 $v \in V$ 를 독립적으로 $min(1, 3CM \ln n/r)$ 의 확률로 샘플링하고, 샘플링된 정점들의 집합을 $H$ 로 하자. 충분히 높은 확률로 $|H| = \tilde{O}(nM/r)$ 이다.
$u, v, x \in V$ 를 고정시켰을 때, $H \cap mid(p) \neq \emptyset$ 일 확률은 $1 - (1 - 3CM \ln n / r)^{r / 3M} \geq 1 - 1/n^C$ 이다. 이를 모든 $P$ 에 속하는 $O(n^4)$ 개의 후보에 대해서 합하면, 높은 확률로 $H \cap mid(p) = \neq \emptyset$ 이 모든 $p \in P$ 에 대해서 성립한다.
이제 $Extend(D)$ 의 쿼리 알고리즘은 다음과 같다. 쿼리 $(u, v, x)$ 가 주어지면, $D(u, v, x) < r$ 일 경우 $D(u, v, x)$ 를 반환한다. 아닐 경우:
$min((3/2)r, min_{h \in H}(D(u, h, x) + D(h, v, x)))$
를 반환한다. $\blacksquare$
이 두 Lemma를 사용하면 Full DSO를 구성할 수 있다. 초기 주어진 $r$-truncated DSO를 $D^{start}$ 라고 하자. Lemma 3.7에 의해 쿼리 시간 $O(1)$ 인 $r$-truncated DSO $D_0 = Fast(D^{start})$ 을 만들 수 있다. $D_0$ 을 사용하여, 쿼리 시간 $O(1)$ 인 $(3/2)r$-truncated DSO $D_1 = Fast(Extend(D_0))$ 를 만들 수 있다. 이를 반복하면, $(3/2)^i r$-truncated DSO $D_i = Fast(Extend(D_{i-1}))$ 과 같이 계속 DSO의 범위를 넓힐 수 있으며, $i \geq \log_{3/2}(nM/r) $ 일 경우 Full DSO를 만들 수 있다. 다시 말해, $D^{final}$이 원하는 DSO라고 하면,
$D^{final} = Fast(Extend(Fast(Extend(\cdots Fast(D^{start})))))$
이다.
3.3.1 Proof of Theorem 1
$O(1)$ 쿼리를 지원하는 Full DSO를 구성했으니, 이것이 $O(n^{2.5794}M)$ 시간에 전처리됨만을 보이면 Theorem 1의 증명이 완성된다.
$\omega(a, b, c)$ 를, $n^a \times n^b$ 행렬과 $n^b \times n^c$ 행렬을 곱할 때 드는 시간 복잡도 $O(n^e)$ 의 exponent $e$ 라고 정의하자. 예를 들어 $\omega(1, 1, 1) \le 2.372.. = \omega $ 이다. 편의상 $\omega(1,1, \lambda) = \omega(\lambda)$라고 하자. 다음과 같은 Lemma들이 성립한다. (증명은 하지 않는다.)
- 양의 실수 $a, b, c, r$ 에 대해 $r + \omega(a, b, c) \le \omega(a, b+r, c+r)$.
- $f(\tau) = \omega(1, 1 - \tau, 1 - \tau)$ 라고 할 때 ($\tau \in [0, 1]$) $\tau + f(\tau)$ 는 단조 비증가하고, $2\tau + f(\tau)$ 는 단조 비감소한다.
$\alpha \in [0, 1]$에 대해, $r = Mn^{\alpha}$ 라고 두자. $\alpha$ 의 값은 이후 정한다. $\mu = 0.5286...$ 이라 두자. (Shortest path tree 구성에 필요했던 상수이다.)
Lemma 3.6, 3.7에서 설명한 중간 과정을 모두 포함해서 $D^{final}$ 의 전처리 시간을 표현하면:
$\tilde{O}(n^{2 + \alpha} M + n^{\omega} M + n^{2 + \mu} M) + n^{2\alpha + \omega(1, 1 - \alpha, 1 - \alpha) + o(1)} M + \sum_{i = 0}^{\lceil \log_{3/2}(nM/r) \rceil} \tilde{O}(\frac{n^{3 - \alpha} M}{(3/2)^i})$
$\le n^{max(2 + \alpha, 2 + \mu, 3 - \alpha, 2 \alpha + \omega(1, 1 - \alpha, 1 - \alpha)) + o(1)} M$
$\alpha = 0.420645, \beta = \frac{1}{1 - \alpha}$ 라고 하자. $1.5 < \beta < 1.75$ 이다. 이 때
$\omega(1, 1 - \alpha, 1 - \alpha) = (1 - \alpha) \omega(\beta) \ \le (1 - \alpha) \frac{(1.75 - \beta)\omega(1.5) + (\beta - 1.5)\omega(1.75)}{1.75 - 1.5} \ \le 0.579355 * 4 * (0.923943 \omega(1.5) + 0.226058 \omega(1.75)) $
2018년 기준 $\omega(1.5) \le 2.796537, \omega(1.75) \le 3.021591$ 이다. 고로
$2\alpha + \omega(1, 1 - \alpha, 1 - \alpha) \le 2.579384$ $\blacksquare$
'공부 > CS theory' 카테고리의 다른 글
| Congestion Balancing (0) | 2022.06.02 |
|---|---|
| Efficient Primal-Dual Algorithms for MapReduce (0) | 2022.01.08 |
| Incremental Topological Ordering and Strong Component Maintenance (0) | 2021.06.27 |
| Expander Decomposition and Pruning: Faster, Stronger, and Simpler (0) | 2021.04.01 |
| Weighted Min-Cut: Sequential, Cut-Query and Streaming Algorithms (2) | 2020.07.24 |
- Total
- Today
- Yesterday
