티스토리 뷰
추석에 BOJ에서 13문제 연습 셋을 만들고 풀기로 결심했다. 아직은 그렇다 ㅋㅋ!
문제
- A. Bridge Park
- B. Kangaroos
- C. Hotline
- D. Justice for All
- E. Farm and Factory
- F. Longest Rivers
- G. Conquer The World
- H. Uncrossed Knight's Tour
- I. Hashigo Sama
- J. 빛의 왕과 거울의 미로 1
- K. 빛의 왕과 거울의 미로 2
- L. Celtic Knots
- M. Farm Village
9월 9일

K. 빛의 왕과 거울의 미로 2
비트 DP와 비슷한 식으로 한 줄에 대한 상태를 저장하는데, 단순한 불리언 변수로는 부족하니까 연결 상태에 대한 union-find를 메모이제이션하는 느낌으로 해결할 수 있는 문제다. 최근에 jh05013님이 Connection Profile DP라는 이름으로 포스팅하였으니 이 글을 참고하면 좋을 것 같다.
시작점과 끝점이 아주 판타스틱하게 주어지기 때문에 고통스러울 것이라고 예상했으나, 짜 보니 그렇게 힘들지는 않은 문제였다. 그래도 다이아 1 정도는 되는 거 같다. 암튼 채널보단 확실히 쉽다.
9월 11일

A. Bridge Park
옛날에 풀이까지 알고 있던 문제였으나 다 까먹어서 다시 생각했다. 그래도 대충 키워드를 알아서 금방 생각한듯..
새로 잇는 간선이 $(i, (i+1) \mod n)$ 만을 잇는다고 생각해 줄 수 있다. 증명은 모르겠는데 그냥 대충 해 보면 다른 경우에서는 이상하다는 것을 알 수 있다. 자명히 그냥 다 이으면 낭비가 심하다. 근데 일단 이어지지 않은 걸 다 이어주고 생각해 보자. Outer face에 모든 정점이 다 닿으면 Dual은 트리이다. 간선을 지우면 특정한 face가 외면에 "노출"된다. 에지의 양 쪽 face가 외면에 "노출"된 것이 그 에지가 Bridge인 것과 필요충분이다. 고로 간선을 최소로 추가해서 = 어떠한 face를 외면으로부터 막아서, 모든 에지에 대해 양 쪽 face중 하나가 노출되지 않도록 해야 한다. Outer face에 관해서 몇 가지 처리해야 할 사항이 있으나 결론적으로 이는 Minimum Vertex Cover 문제여서 트리 DP로 해결된다.
참 좋은 문제다.
D. Justice for All
Constructive라 쫄았는데 생각보다 어렵지 않았다. Typical한, $n$ 짜리 그래프로 $2n, 2n+1$ 만들기가 된다. $2n$ 은 그냥 길이 4의 사이클을 만들어 주면 되니까 쉽다. $2n+1$ 을 하려면 $2n$ 을 하면서 추가적인 매칭을 하나 더 이어줘야 한다. 사이클을 만들 때 그냥 만들지 말고 기존 컴포넌트에 연결되게 붙여주자 ($(n - 1, n)$ 같은 절선 간선을 하나 넣어서) 이제 $(1, n)$ 사이에 에지를 이이어 주자. 절선 간선을 이쁘게 넣어주면, 이 $(1, n)$ 간선을 사용하는 유일한 완벽 매칭이 하나 추가된다.
E. Farm and Factory
잘 안돼서 풀이를 봤는데 뭔가 모델링 자체가 좀 이상했던 듯... 일단 Farm만 있다고 하자. Dijkstra를 돌려주면, $C_u + C_v + dist(1, v) \geq dist(1, u)$ 같은 식이 나온다. 이를 모든 $u, v$ 에 대해서 정리하면 대략 다음과 같은 문제가 된다.
일직선 상 $x = dist(1, i)$ 위치에 점이 $N$ 개 있다. 이들을 중심으로 하는 구간을 각각 만들어서, 구간 길이 합을 최소로 해 주면서 모든 구간이 겹치게 할 수 있을까?
겹치는 점을 $dist(1, i)$ 의 중간값으로 잡아주면 된다. Factory가 있을 때도 비슷한데, 이 때는 45도 축변환 아이디어가 필요하다.
9월 12일
문제를 풀려고 시도했으나 한 문제도 풀지 못했다.
9월 13일

바빠서 많이 풀지는 못했다.
M. Farm Village
전날에 고생했던 문제인데 오늘 보니까 그렇게 어렵지 않았다. 이러한 유형의 문제에서는 MCMF를 진짜 돌리는 그리디 풀이법도 있고, DP 함수의 볼록성을 사용한 slope trick 풀이도 있다. 이 문제에서는 slope trick을 사용하여 DP 배열의 변홧값 배열을 관리하면 Heap만 사용해서 관리가 되어서 그렇게 했다. 볼록함수에서 DP 돌리는 것에 뭔가 심오한 게 있는 것 같은데 최근 좀 알아봐야 겠다는 생각을 했다..
9월 14일
일과 시간엔 바빴고, 밤에는 코드포스만 참가하고 잤다.

- 속도와 정확도가 끔찍하다. 이제 와서 뭐 어떻게 할 생각은 딱히 없다...
- 뒤쪽 문제가 재밌었는데, 앞에서 문제를 푸는데 너무 오래 걸려서 시간이 부족했다.
- 놀랍게도 레이팅이 올랐다고 한다 (+31)
9월 15일
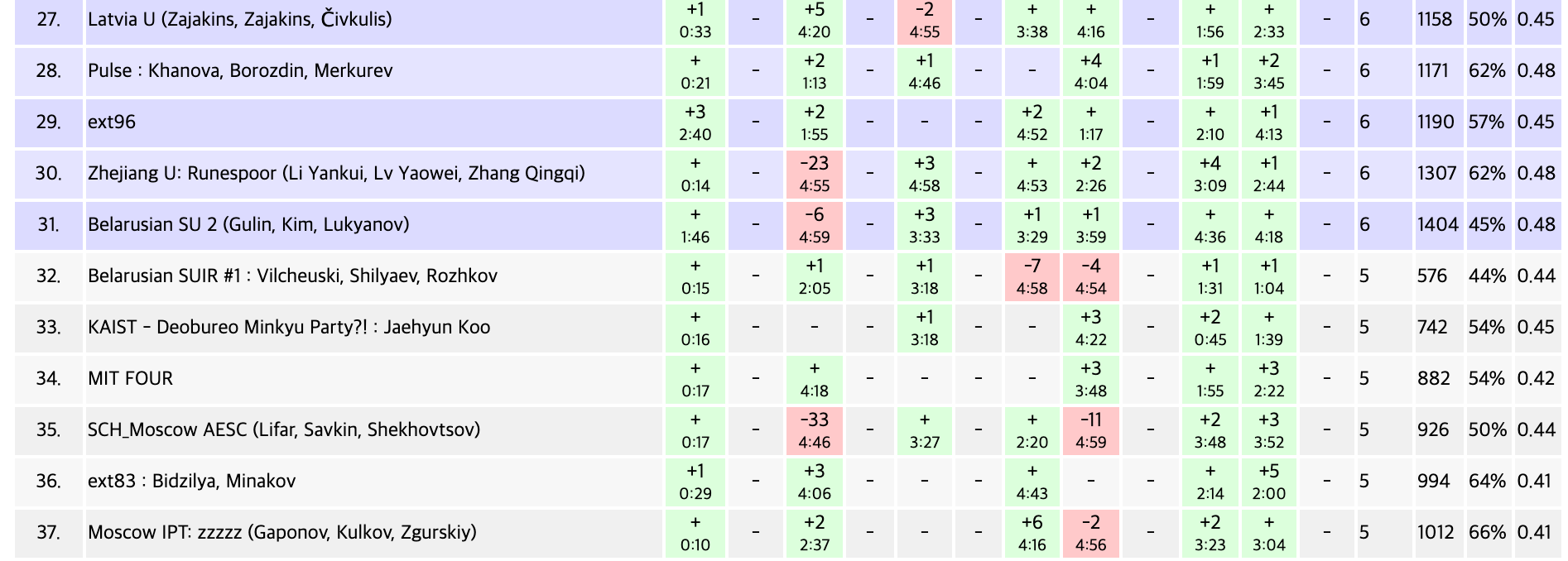
GP of Warsaw를 참가했다.
- B. upsolve해야함
- E. 포함배제를 DP로 하면 n^4인데 랜덤 데이터라서 n^3에 맞는다.
- H. CERC 2017 Gambling Guide처럼 하면 되는데 확률 식이 더러워서 좀 힘들다.
- I. upsolve해야함. 트리에 여러 개의 원이 있을 때, 이것의 교집합은 상당히 더럽지만 어쨌든 원의 형태로 나온다. 합집합의 경우는 정말 많이 더럽고 힘들지만, 어떻게든 하면 된다. 이 문제를 원의 합집합으로 환원하는 것은 쉬워서, 원의 합집합을 구하는 문제를 쉽게 푸는 방법을 오래 생각했으나 찾지 못했다. 알고 보니 원의 합집합을 쉽게 구하는 방법은 딱히 없고, 교집합을 구하는 문제로 환원할 수 있어서 Centroid decomposition으로 풀 수 있는 문제였다. 환원 과정이 나름 신기했던 재밌는 문제. (2시간에 퍼솔이 나왔을 때 정신을 차렸어야 하는데 ㅠㅠ)
- J. good joke.
- K. Failure function을 링크 컷으로 관리하면 된다. 초반부터 많이 풀려서 링크 컷을 안 쓰고 쉽게 할 수 있는 방법을 오랫동안 고민했는데 찾지 못했다. 그리고 포기한 후 링크 컷을 짰는데 정작 10분 정도밖에 안 걸렸다. 처음부터 뇌절했으면 차라리 나았을 듯... 정해는 해싱으로 $N^{1.5}$ 정도에 하는 거고, 잘 이해는 안 가지만 상수가 적으면 $O(N^{1.5}\log N)$ 도 통과하나 보다.
9월 16일
300iq와 함께 2015-2016 Petrozavodsk Winter Training Camp, Moscow SU Trinity Contest 를 돌았다.

- C E F G 를 풀고 B를 틀렸다. 사실 한 게 없다.
- B는 voronoi diagram이랑 똑같이 하면 되는 줄 알았는데 무슨 Radical axis 라는 평생 듣도보도 못한 걸 써야 풀리는 문제였던 거 같다.
- C는 이상한 낚시 문제
- D는 suffix tree에 hld를 쓰면 된다고 한다. well known in russia라고 하는데 전혀 모르겠다..
- E는 지문 읽는 게 어려운 문제
- F는 트리에서 Mo's algorithm을 하면 된다.
- G는 완전 그래프를 만든 후 잘 칠하면 된다.
- 적고 보니까 진짜 한 거 없네 ㅋㅋ; 아무튼 B D 빼면 어려운 셋은 아닌 거 같다.
9월 17일
Hashigo Sama를 어떻게 구현할 지 오랫동안 생각하다가. 코딩을 조금 시작하니 밤이 되어서 잤다.
9월 18일

I. Hashigo Sama
그리고 짜서 맞았다. 문제에서 구현을 간략화하려고 노력한 부분이 많아 보였으나 (예를 들어 컴포넌트를 만드는 방식 때문에 명확한 connection profile을 들고 있을 필요가 없다) 그럼에도 짤 게 많고 고려할 것도 많아서 까다로운 문제였다. 마지막에서도 한 가지 처리를 안 해 준 것을, 아주 열심히 디버깅하여 찾으니 대략 그거 고치는데 2시간 정도... 걸렸다. 하여튼 짜면 뿌듯한 문제. 이 문제에서 제대로 된 구현 청사진을 갖추고 코딩을 시작하는 것은 필수이다.
9월 19일
20일날 Uncrossed Knight's Tour와 선전포고를 했다.
한편, 300iq Contest 2의 Apollonian Network를 풀기 위해 Chordal Graph에 대해서 열심히 공부했으나 잘 이해가 안 돼서 그냥 문제를 풀었다.
F. Longest Rivers

-
강 하나를 고정시켰을 때 이 강의 최대 rank는 $O(n)$ 에 알 수 있다. 당연히 이 강은 루트까지 가야 한다. 고로 강에서 루트까지의 선택은 고정된다. 루트 - 해당 리프 경로가 아닌 곳에 대해서 어떠한 강을 부모 쪽으로 올려야 할 지 결정해야 한다. 해당 강의 길이를 $D$ 라고 할 때, 우리는 $D$ 초과의 강의 개수를 최소화하고 싶다. 만약 자식 중 길이가 $D$ 초과인 게 있으면 그것을 보내고, 아니면 그 중 가장 길이가 작은 것을 보내는 그리디 전략을 사용할 수 있다. 시간 복잡도는 $O(n^2)$ 이다.
-
위 전략은 루트 - 리프 경로에 대해서 일종의 "예외 처리" 를 두기 때문에 최적화하기 껄끄럽다. 만약에 "예외 처리"가 없다면, 즉 $D$ 초과/이하로 자르는 전략은 유지하되, 강에서 루트까지의 선택을 고정하지 않고 거기서도 해당 전략을 쓰는 것이다. 그리고 $D$ 초과인 것의 개수를 세는 것이다. 당연히 이렇게 하면 $D$ 초과인 것의 개수가 늘지는 않는다. 이를 최소화하는 전략이기 때문이다. 그렇다면, $D$ 초과인 것의 개수가 우리가 원하는 것보다 줄어들까? 루트-리프 경로에서, 강이 선택되지 않는 위치부터 차근차근 올라가자. 만약 강 대신 다른 $D$ 이하의 경로가 걸렸다면, 이 경로는 최솟값이니까 강보다 길이가 작고, 어떻게 돼도 $D$ 초과가 되지는 않는다. 고로 이 경로를 우리가 원하는 강으로 바꿔주자. $D$ 초과의 경로가 걸렸다면, 여기서 잘라도 개수는 똑같다. 이 과정을 반복하면 강의 개수를 늘리지 않고 예외 처리 상태의 상황으로 돌아간다. 고로 줄어든다고 가정하면 모순이니 그런 일은 일어나지 않는다.
-
이제 어떠한 고정된 $D$ 후보에 대해서 빠르게 시뮬레이션하는 문제가 된다. $D = 0$ 에서 시작해서 순서대로 늘려가면서 변화하는 값을 "적당히 잘" 관리하는 식으로 풀이를 전개해 보자.
-
$D$를 초과한 강의 개수를 세는 다른 방법이 있다. 각각의 간선에 대해서, 해당 간선이 속한 강이 정확히 그 간선을 지났을 때 $D$를 초과한다면 (즉 간선의 아래쪽 깊이는 $D$ 이하이고 위쪽은 $D$ 초과라면) 해당 간선은 나쁜 강의 개수를 늘려주는 간선이라. 그러한 간선의 개수를 합하면 된다.
-
이러한 느낌으로 간선을 세 가지 상태로 분류하자.
- 해당 간선이 속한 강이, 그 간선을 지나기 전부터 $D$ 를 초과함
- 해당 간선이 속한 강이, 그 간선을 지나기 전에는 $D$ 이하였지만, 그 간선을 지나 올라가면 $D$ 를 초과함
- 해당 간선이 속한 강은 지나 올라가도 $D$ 이하임.
답은 2번 간선의 개수와 동일하다! 정점은, 해당 정점에서 루트로 올라가는 간선이 1번 상태이면 $D$ 초과인 아무거나, 2/3번 상태이면 최솟값을 뽑는다.
-
초기 리프 부모를 잇는 간선은 2번이고 그 외 모든 간선의 상태는 1번이다. 최후 모든 간선의 상태는 3번이다. 3번 상태에 한번 진입한 간선은 다시 다른 상태로 바뀌지 않는다. 2번 상태에 한번 진입한 간선은 3번 상태로만 바뀐다. 고로, 뒤쪽 상태로 갈 수록 후반에 다다르는 것이다. 어떠한 간선이 3번 상태이면, 그 아래에 있는 정점들은 모두 최댓값만 뽑는다. 고로 어떠한 간선이 3번 상태인지 아닌지는 $D$ 에 따라 쉽게 판단된다. 어떠한 간선이 1번 상태에서 2번 상태로 갔다는 것은, 아래 노드 서브트리 내에 있는 모든 자식들이 최솟값을 뽑고 있으며 자신만 최댓값을 취한다는 것이다. 고로 이벤트가 언제 일어나는 지를 $O(n)$ DP로 전부 알아낼 수 있고, 실제 간선이 바뀌는 시뮬레이션은 정렬 + heap 선에서 완성할 수 있다.
9월 20일
언크로스드 나이트 투어와 9시간 정도 치열한 전투를 펼쳤고 패배했다 (...) 자기 전 모범 코드를 읽었는데, 추가적인 커팅이 몇 개 들어가 있는 것으로 보였다. 커팅 비슷한 걸 넣으니까 그 전에 비해서는 훨씬 빨라졌고 (하지만 모범 풀이에 나온대로 8 x 50이 몇초안에 나오진 않는다. 한 몇시간 정도는 필요할듯) 그걸 돌리다 잤다. 언크나투는 내가 잡기에도 너무 쓰레기 문제인 거 같다 (...)
9월 21일
오늘이 마지막 날이다. 전날 돌린 언크나투 프로그램을 이 표랑 대조해 보니까 $m = 7, n = 30$ 근처에서 답이 틀렸다 (...) 외출해야 할 일이 있어서 일과 중에는 다른 걸 하고, 갔다 와서 버그를 찾아서 고친 후 프로그램을 돌려놓고 AGC를 쳤다.
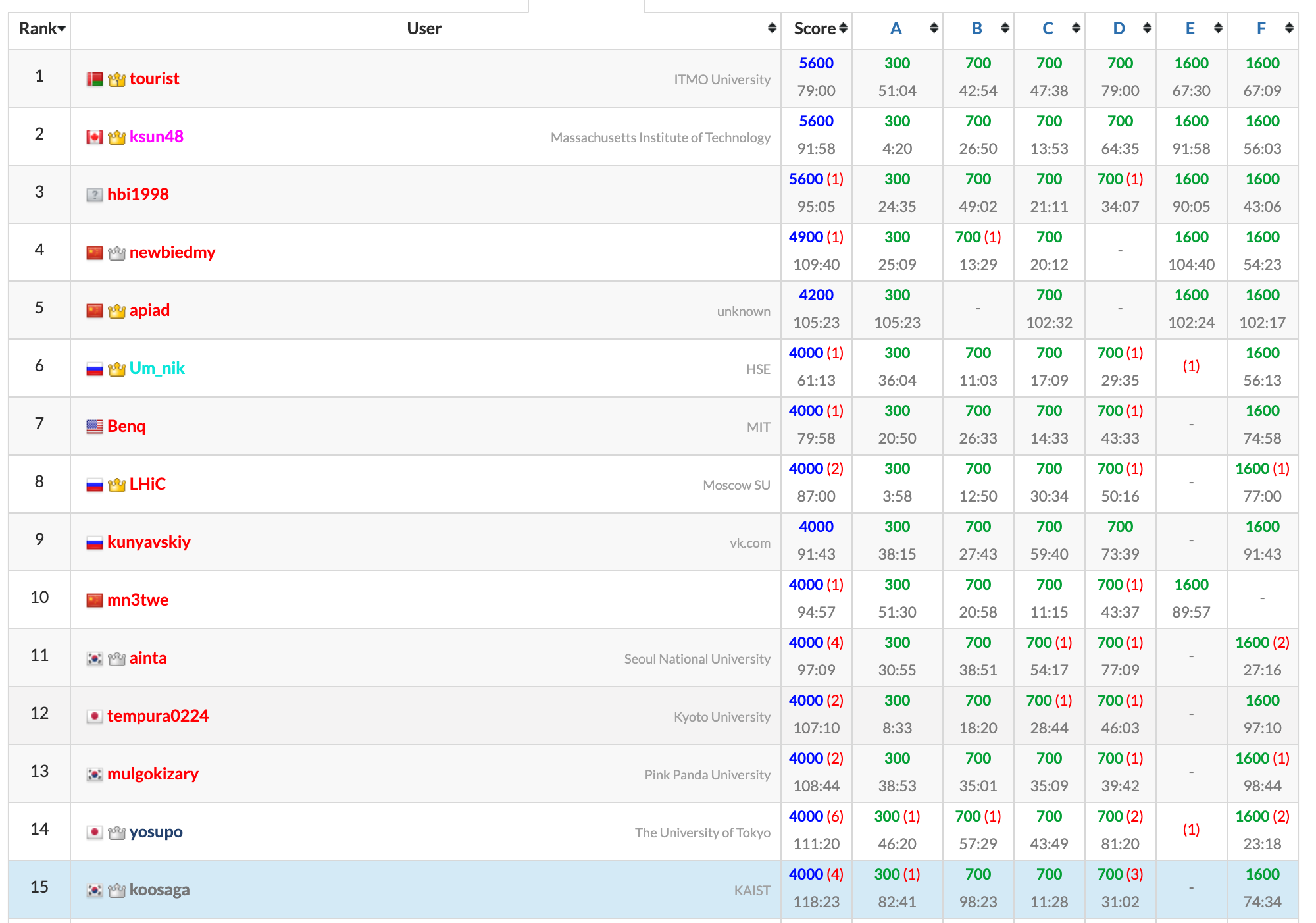
AGC에서는 F가 재밌었다. 시간 제한 때문에 (...) Min-cut 문제임은 명확했는데, 정확히 그래프를 어떻게 구성해야 할지 헷갈렸다. 그 외 문제는 생각보다 별로.
AGC를 한 이후 6시간 쯤 돌리니까 generator가 점화식을 꽤 길게 찾아놨다. $m = 7$ 은 점화식이 명확할 정도로 긴 값이 나왔고, $m = 8$은 그렇지는 않았지만, 유일한 점화식 선택지를 하나 찍으니까 답이 나왔다. 고로 AC.

'공부 > Problem solving' 카테고리의 다른 글
| 2019.12.03 problem solving (3) | 2019.12.03 |
|---|---|
| 장애물을 포함하지 않는 가장 큰 직사각형 찾기 (15) | 2019.10.21 |
| IOI 2019 Day 2 (2) | 2019.08.19 |
| IOI 2019 Day 1 (2) | 2019.08.14 |
| 2019 한국정보올림피아드(KOI) 고등부 문제 풀이 (9) | 2019.07.22 |
- Total
- Today
- Yesterday
