티스토리 뷰
IOI 2019 Day 1 대회가 종료되었다.
한국 학생들의 성적은 다음과 같다. Day 1 기준이고, Day 2 점수를 감안하지 않았음을 유념하라.
- 김세빈, 100 / 100 / 40, 240점, 8등 - 25등
- 윤교준, 72 / 100 / 40, 212점, 26등 - 59등
- 임유진, 72 / 100 / 40, 212점, 26등 - 59등
- 이온조, 38 / 100 / 64, 202점, 60등
올해도 미국의 Benjamin Qi가 만점인 300점을 3시간 30분만에 얻었다. 문제가 쉽지 않았음에도 불구하고 빠른 시간 안에 300점을 얻은 것이 놀라울 따름이다. 단순히 Day1에서 큰 점수차를 보여줬을 뿐만 아니라 실질적으로 다른 학생들과 실력 격차가 크다는 것을 증명했다고 생각한다. 2019년 2연속 우승이 기대된다.
한국은 상당히 좋은 성적을 얻었던 작년의 Day1 결과와 비교하면 훨씬 더 좋은 성적이 나왔음을 알 수 있다. 항상 Day1 문제에 약하다는 징크스(인지 과학인지..) 가 반영된 결과라고도 생각하지만, 대다수의 학생들이 받아야 할 점수 그 이상을 받아주었다는 사실은 부정할 수 없다. Day 2에도 동요하지 않고 좋은 결과를 유지할 수 있었으면 좋겠다.
Day 1 Problems
구현한 코드는 (만약 존재한다면) https://github.com/koosaga/olympiad/tree/master/IOI 에 모두 올라와 있다.
Problem 1. Arranging Shoes
Problem
크기 $2N$ 의 정수 배열 $X[0], X[1], \cdots, X[2N-1]$ 이 주어진다. 이 정수들은 0보다 작을 수 있으나 0인 경우는 없다. 정수 배열이 유효하다 는 것은 다음과 같다:
- 모든 $0 \le i < N$ 에 대해, $X[2i] < 0, X[2i+1] > 0, |X[2i]| = |X[2i+1]|$
당신은 주어진 배열에 인접한 쌍을 교환(swap) 하는 연산을 최소 횟수로 해서 이 배열을 유효하게 만들고 싶다. 필요한 연산의 최소 횟수는 얼마인가? (유효하게 만드는 것이 가능한 것은 보장된다.)
Solution
만점 풀이가 잘 안 보일 수 있으나, 생각보다 간단하게 고득점을 받을 수 있어서 만점을 받는 것도 쉽다고 예상할 수 있다. 절반 가량의 참가자들이 풀었지만 실제로 그렇게 쉬운 문제는 아니라고 생각한다. 이러한 류의 그리디 문제가 well-known이기도 하고, 또한 정해의 접근법을 시도해 볼 여지가 충분히 있는 문제라서 많이 풀렸다고 생각한다.
Subtask 1 (10점)
return (s[0] > 0 ? 1 : 0)
Subtask 3 (30점)
모든 신발의 크기가 같은 경우, 결국 숫자를 적당히 재배열해서 $-x, x, -x, x, \cdots$ 와 같은 수열을 만드는 것이 목표가 된다. 0번 위치부터 순서대로 이 수열을 만들어나가자. 각 위치에 수를 배정할 때, 해당 위치에 이미 원하는 숫자 ($x$ 내지는 $-x$) 가 존재한다면 문제가 해결된다. 그렇지 않다면, 오른쪽으로 가면서 가장 가까운 필요한 숫자를 찾아서 나의 위치로 당겨주면 된다.
위와 같은 것을 그대로 구현하면 $O(N^2)$ 인데, 이는 몇 가지 방법으로 최적화 할 수 있다. 가장 직관적인 방법은 std::set 을 사용하는 것이다. 현재 수열이 $x, x, x, x, -x, \cdots$ 라고 하고, 현재 위치에 $-x$ 가 필요하다고 하자. $x, x, x, x, -x, \cdots$ 를 오른쪽에서 왼쪽으로 순서대로 바꿔준다면, 그 결과는 $-x, x, x, x, x, \cdots$ 과 같이 될 것이다. 즉, 원래 $-x$ 가 있던 위치와 현재 위치 말고는 값이 변하지 않는다. 고로 set에 $x$ 와 $-x$ 의 위치들을 각각 저장한 후, 현재 찾은 가장 가까운 $-x$ 의 위치를 찾고, 두 인접하지 않은 위치 사이에 swap을 해준 후, 실제로는 위치를 하나 하나 옮겨줬다고 생각해서 두 위치의 차를 답에 더해주는 방식을 사용할 수 있다. 이렇게 하면 $O(N\log N)$ 알고리즘이 유도된다.
비직관적이지만 간단한 방법은 다음과 같다: $P_0, P_1, \cdots, P_{n-1}$ 을 각 $-x$ 의 위치를 저장하는 정렬된 배열이라고 하자. 정답은 $\sum_{i = 0}^{n-1} |P_i - 2i|$ 이다. 위 방법을 사용하면 이 값이 절대 늘어나는 일이 없고 무조건 1씩 줄기 때문이다.
이 입력이 사실 Subtask 1을 포함하기 때문에, 이를 구현하면 30점을 얻는다.
Subtask 4 (45점)
Subtask 4는 Subtask 3과 똑같은 방식으로 풀린다. 왜냐하면 여기서도 크기를 무시해도 되기 때문이다 (…) 모든 신발의 크기가 같다고 생각하고 Subtask 3의 전략을 그대로 사용하면, 실제로 $X[0], X[n], X[1], X[n+1], \cdots$ 와 같이 매칭이 된다. 고로 입력 상에서 같은 크기인 신발이 인접하게 된다.
Subtask 4만 풀기 위해서는 이것도 가능하다: return (long long)n*(n-1)/2
Subtask 5 (85점)
위 서브태스크들을 풀다 보면 매칭 가능한 가장 가까운 짝신발을 이어주는 전략이 유효함을 알 수 있다. 고로 다음과 같은 알고리즘을 생각할 수 있다:
- 해당 신발과 짝이 맞는 가장 가까운 신발을 반복적으로 매칭 ($O(n^2)$)
- 매칭 이후 오른쪽 신발이 왼쪽 신발 앞에 있다면 교환 (답 1 증가)
짜면 맞기 때문에 별로 증명할 필요는 없고 여기서도 증명을 생략한다… 아무튼 서브태스크 3에서의 "그대로 $O(n^2)$ 구현" 을 사용하면, 일반적인 케이스에서 문제를 해결할 수 있다. 총 85점을 받을 수 있다.
만점 풀이 (100점)
해당 신발과 짝이 맞는 가장 가까운 신발들을 매칭"만" 해 주자. 즉, 왼쪽에서 오른쪽으로 가면서 해당 신발과 짝이 맞는 가장 가까운 신발을 찾아주고, 실제로 교환은 하지 않는 것이다. 실제로 교환을 하지 않는다고 가정하면 이 과정은 $O(N)$ 에 가능하다. 각 크기의 신발에 대해서 따로 따로 매칭을 해 주는데, 단순히 정렬된 순서대로 음수 크기 신발과 짝수 크기 신발 사이에 매칭을 해 주면 되기 때문이다.
이제 매칭을 왼쪽 끝 순서대로 정렬하고 실제로 두 수를 모아주자. 어떠한 두 수를 모은다는 것은 이 두 수를 배열에서 지운다는 것과 유사하다고 생각할 수 있다. 고로, 우리가 실제로 두 수를 모으기 위해 하게 될 일은:
- 두 수 사이에 있는 지워지지 않은 수의 개수를 세고 (이것이 실제로 필요한 swap 횟수가 된다.)
- 오른쪽 신발이 왼쪽 신발 전에 있으면 바꿔준 후
- 두 수를 지우는
이 세가지 연산이 된다. 2번째 연산은 단순하게 하면 되고, 1번째 / 3번째 연산은 크기 $2N$ 크기의 Fenwick tree를 만들어서 할 수 있다. $Alive[x] = (x$ 가 지워지지 않은 원소면 1, 아니면 0) 이라고 정의했을 때, 초기 $Alive[x] = 1$ 이고, 두 수 사이에 있는 지워지지 않은 수의 개수는 $Alive$ 배열의 구간 합으로 표현 가능하고, 두 수를 지우는 것은 어떠한 원소에 대해 $Alive[x] = 0$ 을 설정해 주는 것이기 때문이다. 총 시간 복잡도는 $O(n \log n)$ 이 된다.
Problem 2. Split the Attractions
Problem
$n$ 개의 정점과 $m$ 개의 간선을 가진 무방향 연결 그래프 $G$ 가 주어졌을 때, 모든 정점 집합을 3개의 집합 $A, B, C$ 로 분할해야 한다. 이 때 이 집합은 다음과 같은 조건을 만족해야 한다:
- $A$의 크기는 $a$, $B$ 의 크기는 $b$, $C$ 의 크기는 $c$ . "분할"(partition) 이기 때문에 모든 정점이 $A, B, C$ 중 정확히 하나에만 속해야 한다. 고로 $a + b + c = n$ 을 만족한다.
- $A, B, C$ 중 2개 이상은 연결되어 있어야 한다: 정점 부분집합 $S$가 연결되어 있다는 것은, $S$ 에 속하지 않은 정점과 양 끝점중 하나 이상이 $S$ 에 속하지 않는 간선을 지웠을 때, 그래프가 연결되어 있다는 것을 뜻한다. (간단히 말해서 Induced subgraph $G[S]$ 가 연결 그래프이다.)
이것이 가능한지 판별하고, 가능하다면 그 집합을 반환하라.
Solution
Subtask 1 (7점)
각 관광지의 차수가 최대 2라는 것은, 관광지들이 단순 사이클($m = n$) 이나 직선($m = n-1$) 을 이룬다는 것이다. 단순 사이클을 이루는 경우, 그래프에서 아무 간선이나 지워주면 선이 되니, 일반성을 잃지 않고 입력이 직선이라고 가정하자. 이 경우, 단순히 직선을 $a, b, c$ 크기로 쪼개주면 항상 문제를 해결할 수 있다. 구현은 degree 1인 점을 잡고 깊이 우선 탐색을 통해서 직선을 찾는 것이 가장 간단하다.
Subtask 2 (18점)
먼저 다음과 같은 Lemma를 제시한다:
-
Lemma 1. 일반성을 잃지 않고 $A, B$ 가 연결된 컴포넌트를 이루도록 정한다고 하자. 이 경우, 그래프의 정점 집합을 연결된 두 집합 $A^\prime, B^\prime$ 로 분할해서, $ A^\prime \cup B^\prime = V(G), A^\prime \cap B^\prime= \emptyset, | A^\prime| \geq a, | B^\prime| \geq b$ 를 만족하게끔 할 수 있는 것과, 문제의 정답이 존재하는 것이 동치이다.
-
증명:
- $\rightarrow$: $A^\prime$ 에서 DFS를 한 후, DFS preorder를 구한다. 이 때 맨 앞 $a$개의 정점은 연결 컴포넌트이므로 $A$ 를 이것으로 둔다. $B$ 에 대해서도 동일한 것이 가능하다. $C = V(G) \setminus A \setminus B$ 라 두면 문제가 해결된다.
- $\leftarrow$: 그래프가 연결이기 때문에, $C$ 에 있는 어떠한 정점을 $A$나 $B$ 한 쪽에 붙이는 것을 반복하여 전부 지워버릴 수 있다. 남은 $A, B$ 는 문제의 조건을 만족한다.
-
Lemma 2. 일반성을 잃지 않고 $a \le b \le c$ 라고 하면, $A, B$ 에 대해서만 해 보아도 된다.
-
증명: $A, B$ 에 대해서 하지 못하면서 $A, C$ 나 $B, C$ 에 대해서 할 수 없다.
아무튼, 이제 문제를 3개의 분할이 아니라 하나의 부분 집합 $S$ 를 찾는 것이라고 볼 수 있다. $S$ 는 연결되어야 하고, $V(G) \setminus S$ 역시 연결되어야 하고, $a \le |S| \le n - b$ 를 만족해야 한다. 이 집합을 주면 위의 Lemma를 증명할 때 썼던 프로시저를 그대로 써서 답을 반환할 수 있으니, 그 프로시저를 $answer(S)$ 라고 구현하고 문제를 해결하자.
이 문제에서는 $|S|$ 의 사이즈에 대한 제약이 없이 위 조건을 만족하는 아무 부분집합이나 잡으면 된다. 여러 선택지가 있겠지만 서브태스크가 $a = 1$ 의 형태이니 $|S| = 1$ 을 시도해 보자. 이 경우, $S$ 의 여집합이 연결되도록 해야 하는데, 이는 Lemma 1의 증명과 똑같이 할 수 있다: 스패닝 트리를 잡은 후, 가장 마지막에 방문한 정점 하나를 $S$ 라고 하면, 이 외 나머지 $n-1$ 개의 정점은 연결되어 있으니 문제의 조건을 만족한다.
Subtask 3 (40점)
그래프가 트리의 형태일 경우, 트리를 두 연결된 컴포넌트로 나누는 방법은 간선 하나를 자르는 방법밖에 없다: 0번 정점을 루트라고 하고, $A$ 가 0번 정점을 포함한다고 하였을 때, $B$ 에 포함되면서 0번 정점과 가장 가까운 점을 생각해 보았을 때, 이 정점 아래 서브트리에 있는 정점은 모두 $B$ 에 포함되고, 그러한 정점만 $B$ 에 포함될 수 있다. 고로 트리 상에서 두 연결된 컴포넌트는 간선 하나로 분리할 수 있다.
이제 문제를 해결하는 것은 그다지 어렵지 않다. 간선 하나를 제거했을 때 각 컴포넌트의 크기를 알 수 있다면 문제를 바로 해결할 수 있기 때문이다. 아무 정점을 루트로 잡은 후 트리를 깊이 우선 탐색으로 탐색하면서, 해당 정점의 서브트리 안에 있는 정점의 개수를 관리하자. 이 값을 안다면, $parent(v) - v$ 간선을 지웠을 때 각 컴포넌트의 사이즈는 $v$ 의 서브트리 사이즈를 통해서 유추할 수 있다. 이것이 $a, b$ 혹은 $b, a$ 보다 크다면 $answer$ 함수에 서브트리 정점들을 모아서 호출해 주면 되고, 아닐 경우 위 관찰에 의해서 답이 존재하지 않는다.
만점 풀이
64점 풀이는 정말 잘 모르기 때문에 만점 풀이로 넘어간다. 의도된 만점 풀이는 전혀 직관적이지 않지만 매우 아름답다. 출제자에게 경의를 표한다.
일단 한동안은 그래프가 트리라는 가정을 그대로 유지하자. 가장 먼저 관찰해야 할 것은 $a \le n / 3, b \le (n - a)/ 2$ 라는 사실이다. 이 두 사실은 $a \le b \le c$ 라는 부등식과 $a + b + c = n$ 이라는 성질에서 바로 유도할 수 있다. 또한 이 사실을 통해서 다음과 같은 Lemma를 유도할 수 있다.
Lemma 3. 트리의 Centroid를 잡고, Centroid에 인접한 간선들만 끊어 봐도 문제를 해결하는 데 충분하다.
Proof. 끊은 간선이 Centroid에 인접하지 않다고 하자. Centroid를 포함하는 쪽을 $B$, 아닌 쪽을 $A$ 라고 생각할 수 있다. 이 때 끊은 간선을 Centroid에 가까워지는 방향으로 계속 옮겨 주면, $A$ 의 크기는 계속 증가하고, $B$ 의 크기는 계속 $n/2$ 이상으로 유지된다.
많이 갑작스럽지만, 그래프에서 아무 스패닝 트리나 잡고 비슷하게 문제가 해결되기를 기도해 보자. 아무 스패닝 트리를 잡은 후 이 스패닝 트리의 Centroid를 중심으로 잡고 문제를 해결해 보자. 확실하게 알 수 있는 사실은, Centroid를 트리에서 지웠을 때 $a$ 이상의 크기를 가지는 서브트리가 존재한다면, 트리 케이스와 동일하게 해당 서브트리를 잘라서 문제를 바로 해결할 수 있다는 것이다.
이제 문제가 해결되지 않은 경우는, Centroid를 지웠을 때 모든 서브트리의 크기가 $a$ 미만인 경우이다. 앞선 경우와 다르게 이번에는 이러한 상황에서도 문제가 해결될 수 있는 여지가 있다. 이유는 스패닝 트리에 포함되지 않은 간선들이 이 서브트리들을 연결시킬 수 있기 때문이다.
해당 Centroid를 지운 후 남은 서브트리들을 모두 하나의 정점으로 묶어서 생각하자. 각 정점에는 해당 서브트리에 원래 있던 정점의 개수를 가중치로 설정한다. 고로 우리는 모든 정점의 가중치가 $a$ 미만인 어떤 그래프를 만들 수 있다. 이렇게 만든 그래프가 연결되어 있을 이유는 없다는 데에 유의하라 (예를 들어 centroid가 절점일 경우 확실히 연결이 아니다).
이 그래프에 대해서도 앞과 비슷한 것을 알아낼 수 있는데, 바로 그래프의 연결 컴포넌트의 크기가 모두 $a$ 미만일 경우 답이 존재하지 않는다는 것이다. 이유는 다음과 같다. 두 연결 컴포넌트 중 하나는 Centroid를 포함하지 않는데, Centroid를 포함하지 않는 컴포넌트는 그래프에 주어진 연결 컴포넌트 중 단 하나만을 고를 수 있다. 고로 어떻게 골라도 컴포넌트의 크기가 $a$ 미만일 경우 문제의 답이 존재하지 않는다.
이제 그렇지 않은 경우 항상 답이 있음 을 보인다. 그래프의 연결 컴포넌트의 크기가 $a$ 이상인 것을 아무거나 하나 고른다. 어떠한 정점을 잡고 깊이 우선 탐색을 한 후, DFS preorder 상에서 가중치 합이 $a$ 이상인 가장 짧은 prefix를 아무거나 택해서 그것을 $A$ 라고 하고 나머지를 $B$ 라고 하자. 확실하게 $A$ 는 연결되어 있고, $B$ 는 centroid를 포함하기 때문에 역시 연결되어 있다. 이제 우리는 $a \le |A| \le 2a - 2$ 임을 알 수 있는데, 해당 prefix의 마지막 원소를 제외한 것의 크기가 $a - 1$ 이하이고, 그리고 마지막 원소의 크기 역시 $a - 1$ 이하이기 때문이다. $B$ 의 크기는 $n - 2a + 2$ 이상인데, $n - 2a + 2 \geq b$ 가 무조건 만족된다. $a \le c$ 이기 때문에, $2a + b \le a + b + c \le n + 2$ 가 성립하기 때문이다. 고로 원하는 모든 조건이 만족되었고, 이를 구현하면 100점을 받을 수 있다.
Problem 3. Rectangles
Problem
$N \times M$ 크기의 2차원 배열 $H$가 주어진다 ($0 \le H[i][j] \le 7,000,000$. 0-based). 직사각형 영역 은 4개의 정수 $x_1, x_2, y_1, y_2$ 로 정의되며, $x_1 \le i \le x_2, y_1 \le j \le y_2$ 를 만족하는 모든 셀 $(i, j)$ 를 포함한다. 이 때 $1 \le x_1 \le x_2 \le N-2, 1 \le y_1 \le y_2 \le M-2$ 이기 때문에 외곽에 있는 셀은 포함할 수 없다.
유효한 직사각형 영역 은, 직사각형 영역 내 모든 셀 $(i, j)$ 에 대해, $min(H[x_1 - 1][j], H[x_2 + 1][j], H[i][y_1 - 1], H[i][y_2 + 1]) > H[i][j]$ 을 만족하는 직사각형 영역을 뜻한다. 모든 가능한 유효한 직사각형 영역의 개수를 반환하라.
Solution
Subtask 1 (7점)
직사각형 영역으로 가능한 모든 $x_1, x_2, y_1, y_2$ 을 나열한 후, 유효한 직사각형 영역의 정의를 만족하는지 단순하게 판별한다. 직사각형 영역으로 가능한 셀의 개수는 $O(n^2m^2)$ 이고 정의를 만족하는지는 문제 지문을 따라하면 $O(nm)$ 에 확인 가능하기 때문에, 전체 문제가 $O(n^3m^3)$ 에 해결된다.
Subtask 2 (15점)
유효한 직사각형 영역을 찾는 조건은 다음과 같이 쓸 수 있다:
- $min(H[x_1 - 1][j], H[x_2 + 1][j]) > H[i][j]$
- $min(H[i][y_1 - 1], H[i][y_2 + 1]) > H[i][j]$
이렇게 되면 각 행과 열에 대해서 문제가 분리된다. $j$ 가 고정되었을 경우 $H[?][j]$ 의 구간 최댓값을 구해서 그것만 비교해도 되고, $i$ 가 고정되었을 경우 마찬가지로 $H[i][?]$ 의 구간 최댓값을 구하면 된다. $RM[i][j][k] = Max_{x = j}^{k} H[i][x] $ 라고 정의하자. 비슷한 방법으로 $CM[i][j][k] = Max_{x=j}^{k}H[x][j]$ 라고도 정의하자. 이 값은 단순한 방법으로 $O(nm(n^2+m^2))$ 에 구할 수 있다. 이제 유효한 직사각형인지 조건을 모든 $i$ 에 대해서 따로, $j$ 에 대해서 따로 판별하면 되니 $O(n+m)$ 에 조건이 확인된다. 전체 문제가 $O(n^2m^2(n+m))$ 에 해결된다.
Subtask 6 (28점)
모든 입력이 0과 1뿐이니 직사각형 경계 밖에 있는 셀은 모두 1이고 안에 있는 셀은 모두 0이어야 한다. 그림으로 그리면 대충 이렇다:
?????????
??11111??
?1000001?
?1000001?
??11111??
?????????
여러가지 방법이 있는데, 가장 간단한 방법은 DFS를 사용하는 것이다. 0으로 이루어진 컴포넌트에 대해서 flood-fill을 한 후, Flood fill된 영역이 유효한 직사각형인지를 판별하는 식의 풀이가 가능하다. 유효한 직사각형인지를 판별하는 것은, 방문한 영역의 행/열 최대/최솟값, 그리고 방문한 영역의 개수를 세어주면 가능하다.
Subtask 3/5 (50점)
Subtask 2의 방법을 최적화하자. 각 행과 열에 대해서 분리해서 생각하는 전략은 그대로 사용한다. 다음과 같이 $LowR[i][j][k]$ 를 전처리하자:
- $LowR[i][j][k] = k$ 행에서 시작하여, $Max_{x = i}^{j}H[k][x] < min(H[k][i-1], H[k][j+1])$ 을 만족할 때까지 계속 $k$ 를 증가시켰을 때 그 결과
열에 대해서도 똑같은 방법으로 $LowC[i][j][k]$ 를 전처리 가능하고, 이에 $O(n^2m^2)$ 의 시간이 소요된다. 이제 한 직사각형이 유효한지를 $O(1)$ 에 판별할 수 있다. $LowR[y_1][y_2][x_1]$ 과 $x_2$ 의 값을 비교하면 모든 행에 대해서 조건이 만족하는 지를 알 수 있다. 반대 방향으로 열에 대해서도 할 수 있다. 고로 시간 복잡도는 $O(n^2m^2)$ 정도이다 (또한 Subtask 5가 자동적으로 해결된다.)
Subtask 4 (72점)
이미 필요로 하는 정보가 너무 많기 때문에 이를 줄여야지 더 큰 입력을 해결할 수 있다는 것을 눈치챌 수 있다. 다행스럽게도 다음과 같은 좋은 성질이 Subtask 4를 해결하는 데 큰 도움이 된다.
행열에 대해서 똑같은 조건을 판단해야 하니, 일단 문제를 간략화하기 위해 행에 대해서만 조건을 고려하고, 그것도 하나의 행에 대해서만 조건을 고려해 보자. 이 행을 $H[0], H[1], \cdots, H[n-1]$ 이라고 하면, 우리가 원하는 것은 $Max_{x=i}^{j} H[x] < min(H[i-1], H[j+1])$ 을 만족하는 쌍 $1 \le i \le j \le n - 2$ 에 대해 관심이 있다.
여기서 중요한 관찰이 있는데, 위 조건을 만족하는 쌍은 $n$ 개를 넘지 않는다. 가장 간단한 설명은 $Max_{x = i}^{j} H[x]$ 의 최댓값을 이루는 $x$ 를 고정시키는 것이다. $x$ 를 고정시켰을 경우, $x$ 왼쪽에 있는 숫자 중 $H[x]$ 초과인 가장 가까운 수, 오른쪽에서 $H[x]$ 초과인 가장 가까운 수를 두개 찾자. 이 두 수가 $i-1, j+1$ 으로 가능한 유일한 후보인 것이, 구간은 이 두 수를 넘어갈 수 없고 (넘어갈 경우 최댓값 조건이 깨짐) 구간은 이 두 수에 무조건 걸쳐야 하기 때문 ($min(H[i-1], H[j+1])$ 이 $H[x]$ 보다 커야 한다) 이기 때문이다. 고로, 각 $x$ 에 대해서 가능한 $i, j$ 는 (만약 존재한다면) 유일하게 결정 가능하며, 이는 stack을 사용하여 $O(n)$ 시간에 찾을 수 있다.
이제 조건을 만족하는 쌍을 각 행과 열에 대해서 선형 시간에 계산해 놓으면, 우리가 고려해야 할 쌍이 모두 $O(nm)$ 개라는 것을 알 수 있다. 숫자가 유의미하게 작아졌기 때문에 이러한 쌍들을 기준으로 생각해 줄 수 있다. 또한, 위에서 사용한 $LowR[i][j][k], LowC[i][j][k]$ 의 정의를 그대로 사용할 수 있는데, 조건을 만족하는 쌍의 개수가 많아야 $O(nm)$ 개이기 때문에, 이들에 대해서만 값을 계산해 주면 나머지의 값은 자명하기 때문이다. 각각의 올바른 $(i, j, k)$ 쌍에 대해서 $(i+1, j, k)$ 쌍이 올바른지는 이분 탐색이나 $N \times N, M\times M$ 버킷을 만드는 식으로 $O(\log NM)$ 내지는 $O(1)$ 에 가능하다.
이제 실제 답을 찾는 것에 주목하자. Subtask 4까지는 이 처리를 상대적으로 단순하게 해도 문제를 해결할 수 있다. 예를 들어, 직사각형의 왼쪽 변 ($r_1, r_2, c_1$) 을 고정시키고 생각해 보자. 왼쪽 변을 고정시키기 위해서는 $c_1$ 열에서 $(r_1, r_2)$ 가 조건을 만족하는 쌍이어야 하기 때문에, 왼쪽 변으로 가능한 후보는 많아야 $O(nm)$ 개이다. 이들에 대해서 이제 $c_2$ 를 증가시키면 되는데, 각 $c_2$ 에 대해서 $LowR[c_1][c_2][r_1]$ 이 $r_2$ 인지를 확인하고 그렇다면 답을 증가시키는 식으로 문제를 해결할 수 있다. 이 때 $c_2$ 로 가능한 경우의 수는 $O(m)$ 이므로 대략 $O(nm(n+m))$ 정도의 시간 복잡도에 풀린다. 이 때, $LowR[c_1][c_2][r_1]$ 값 하나를 $log$ 시간이 아니라 $O(1)$ 시간에 찾도록 잘 조정해야 함에 유의하라. 정렬과 같은 적절한 전처리로 $O(1)$ 시간에 하게끔 할 수 있다.
100점 풀이
두 가지 종류의 풀이를 알고 있다. 하나는 김세빈 학생과 내가 생각한 복잡한 풀이이고, 하나는 임유진 학생과 윤지학 조교가 생각한 상대적으로 간단한 풀이이다 (임유진 학생은 애석하게도 구현 후 TLE를 받았다고 한다. ㅠㅠ..) 두 풀이를 모두 소개한다. Github에 올라온 코드는 복잡한 풀이로 구현되어 있다.
복잡한 풀이 직사각형의 왼쪽 위 모서리 $r_1, c_1$ 을 고정시키자. 모서리를 고정시키면 왼쪽 변으로 올 수 있는 후보와 위쪽 변으로 올 수 있는 후보들의 집합을 알 수 있다. 전자는 $r_2$ 를 고정시키며 후자는 $c_2$ 를 고정시킨다. 첫번째 후보의 개수를 $L$, 두번째 후보의 개수를 $R$ 이라고 하면, 모든 $(r_1, c_1)$ 에 대해서 $L+R$ 의 합은 $O(nm)$ 이니, 적당히 이에 비례하는 시간 복잡도로 문제를 해결하면 된다는 것을 알 수 있다.
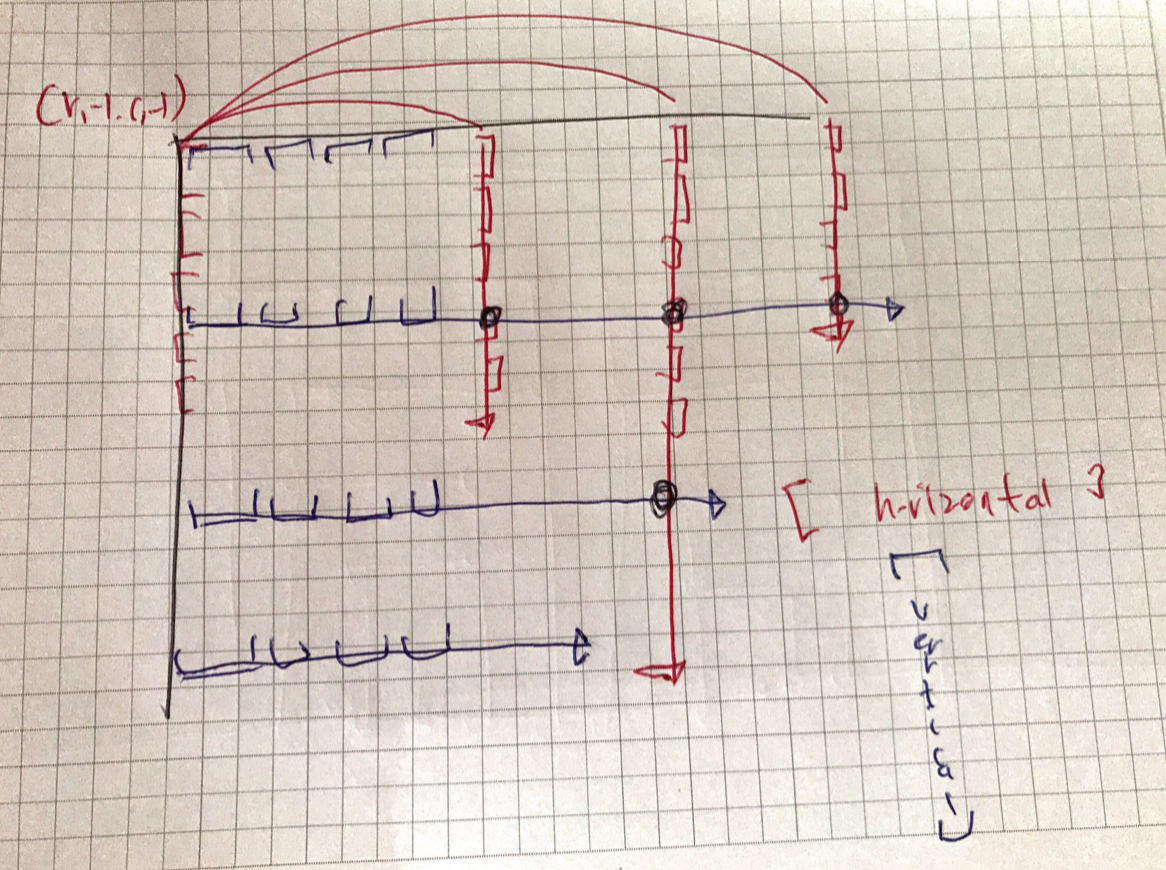
각 왼쪽 변 후보, 위쪽 변 후보에 대해서, 해당 위치에서 직사각형이 얼마나 멀리 갈 수 있는지를 위의 $LowR[i][j][k], LowC[i][j][k]$ 전처리를 통해서 바로 계산할 수 있다. 대충 $(r_1, c_1, r_2)$ 에서 가능한 직사각형의 최대 $c_2$ 를 $f(r_2)$, $(r_1, c_1, c_2)$ 에서의 최대 $r_2$ 를 $g(c_2)$ 라고 하자. 어떠한 직사각형이 유효하기 위해서는, $c_2 \leq f(r_2), r_2 \leq g(c_2)$ 가 만족해야 한다. 이는 사실 다음과 같은 기하 문제로 해석할 수 있다: $(r_2, c_1) - (r_2, f(r_2))$ 을 잇는 가로 선분과, $(c_2, r_1) - (c_2, f(c_2))$ 를 잇는 세로 선분이 존재할 때, 가로 선분과 세로 선분이 교차할 경우 올바른 직사각형을 이룰 수 있으니, 이러한 선분의 교차점의 수를 세는 것이다. 이는 Plane sweeping으로 풀 수 있음이 잘 알려져 있으며, 세로 선분을 $f(c_2)$ 순으로 정렬한 후 행에 대한 fenwick tree를 관리하면 해결할 수 있다.
간단한 풀이 사실 조건을 만족하는 직사각형은 $nm$ 개를 넘지 않는다. 72점 풀이에서 설명한 것과 똑같은 논리가 통하는데, 직사각형 영역 내의 최댓값을 이루는 $(i, j)$ 를 고정시키면, $(i, j)$ 왼쪽, 오른쪽, 위쪽, 아래쪽에 있는 숫자 중 $H[i][j]$ 초과인 가장 가까운 수가 직사각형을 고정한다. 이 네 경계를 넘어가면 최댓값 조건이 깨지고, 이 네 경계에 미치지 못하면 유효한 직사각형이 안 되기 때문이다. 고로, 이러한 최대 $nm$ 개의 직사각형에 대해서 실제 문제의 조건이 만족하는 지를 판별하면 되고, 이는 Subtask 4에서 사용한 방법을 그대로 사용하면 된다 (이 경우에는 이분 탐색을 그대로 사용해도 문제가 없다). 시간 복잡도는 $O(nm \log nm)$ 이다.
여담으로, 임유진 학생의 사례에서 볼 수 있다시피 이 문제는 시간 제한이 널널하지 않은 편에 속한다. 나 역시 같은 복잡도에서 빠른 코드를 짜지 못하는 편이라 맞기까지 고생을 많이 했는데, 상수 최적화를 할 때는 후보들을 정렬할 때 counting sort를 사용해서 $O(NM \log NM)$ 부분을 $O(NM)$ 으로 줄이는 식의 접근을 많이 하였다. (Fenwick tree를 사용하기 때문에 전체 시간 복잡도가 바뀌지는 않는다.) 모범 코드는 상당히 빠른 $O(NM \log NM)$ 으로 구현되어 있으며, $O(NM)$ 으로 쉽게 줄일 수 있는 것 같다.
'공부 > Problem solving' 카테고리의 다른 글
| 2019.09.13 problem solving (3) | 2019.09.12 |
|---|---|
| IOI 2019 Day 2 (2) | 2019.08.19 |
| 2019 한국정보올림피아드(KOI) 고등부 문제 풀이 (9) | 2019.07.22 |
| 2019 한국정보올림피아드(KOI) 중등부 문제 풀이 (0) | 2019.07.22 |
| APIO 2019 (0) | 2019.05.27 |
- Total
- Today
- Yesterday
