티스토리 뷰
IOI 2019 Day 2 대회가 종료되었다. 한국 학생들의 성적은 다음과 같다.
- 김세빈, 100 / 100 / 40 / 72.30 / 66 / 57, 435.30점, Day2 27등, 전체 18등, 금메달.
- 윤교준, 72 / 100 / 40 / 90.97 / 66 / 57, 425.97점, Day2 16등, 전체 22등, 금메달.
- 임유진, 72 / 100 / 40 / 61.41 / 66 / 57, 396.41점, Day2 40등, 전체 37등, 은메달.
- 이온조, 38 / 100 / 64 / 50.61 / 52 / 24, 328.61점, Day2 120등, 전체 83등, 동메달.
미국의 Benjamin Qi는 작년과 같이 이번에도 Day 2에서 조금 노는 (?) 모습을 보였고 1등 성적을 받지 못하였으나, 이미 Day 1에서 상당한 차이를 벌려놓은 이후이기에 안전하게 트로피를 얻었다. 이 외 러시아의 Ildar Gainulin, 캐나다의 Zixiang Zhou이 뒤를 이었다. Ildar Gainulin은 1번의 기회가 남았고, Zixiang Zhou는 3번의 기회가 남았다. 향후 성적이 상당히 주목된다.
한국은 총 금메달 2개, 은메달 1개, 동메달 1개로 국가순위 4등의 성적을 얻었다. 성적은 2013년 이후 한국 팀이 평균적으로 받는 수준과 유사하다. 더 잘할 수 있었던 팀인 것 같아서 아쉽지만 (특히 동메달 1등을 한 이온조 학생이 많이 안타까울 것 같다. 유감을…) 만족스러운 결과를 얻은 한국 팀 축하합니다!
Day 2 Notice
Problem 4. Broken Line
2차원 평면 상에 $N$ 개의 점이 주어진다. 각 점은 양의 정수인 $x, y$ 좌표를 가지고 있으며, 임의의 서로 다른 두 점이 같은 $x$ 좌표를 공유하지 않고, 임의의 서로 다른 두 점이 같은 $y$ 좌표를 공유하지 않는다. 당신은 (0, 0)에서 시작하는 꺾인 선 (Broken Line)을 그을 것이다. 꺾인 선은 항상 $X$ 축 혹은 $Y$ 축에 평행해야 하며, 그 외 다른 조건은 없다 (자신과 겹치거나 교차해도 된다). 당신은 하나의 꺾인 선 을 그어서 모든 점을 꺾인 선과 닿게끔 하고 싶으며 (끝점에 닿아도 닿는 것으로 간주한다) 이 과정에서 선이 꺾이는 횟수를 가능한 작게 유지하려고 한다.
이 문제는 Output Only 문제로, 오직 10개의 테스트 데이터에 대해서만 채점되며 이 테스트 데이터는 모두 사전공개되어 있다. (IOI 2017 Nowruz와 다르게 테스트 데이터의 실제 구성이 크게 중요하지는 않기 때문에 이에 대해서는 서술하지 않는다. 다만 영국 국기 모양 등 특수한 테스트 데이터들이 존재했다고 들었다.) 채점 기준은 복잡하니 실제 PDF를 확인하는 것을 추천한다.
Solution
Broken Line은 Output-only 문제이지만, 2010년 Maze, 2017년 Nowruz와는 상황이 다른 면이 있다. 이전의 경우에는 주최 측에서도 주어진 문제를 제대로 풀지 못하여서, 단순히 모범 코드가 풀 수 있는 테스트 데이터만을 제공하거나 (Nowruz) 아예 그 조차도 아닌 (Maze), 과학 올림피아드 대회에 적절하지 않은 문제들이었다.
이번 Broken Line은 주최에서 모든 입력에 대해서 100점을 받을 수 있는 풀이를 가지고 있음에도 불구하고, Output-only로 문제가 제시되었다. 다른 기하 문제들과 비슷하게 문제가 테스트 데이터 없이는 상당히 까다롭고, 또한 Visualizer를 주는 것이 도움이 된다고 판단했던 것 같다. 하지만 Output-only 문제의 고질적인 맹점인 휴리스틱의 통과는 막지 못하였던 것 같다. 이러한 점에서 이 문제는 2010 maze / 2017 nowruz보다는 2015 scales와 더 유사한 면이 있다 (적절한 휴리스틱을 사용하였을 때 점수를 더 얻을 수 있음). 물론, 2015 scales의 경우는 휴리스틱을 사용해서 점수를 많이 받기는 어려운 문제였음을 고려해야 한다.
Output-only 형태로 문제를 제시하는 것이 주는 이점이 존재하고 고려할 만하다고 보지만, 비과학적인 풀이가 통과하는 상황을 막지 못한 것은 아쉽다. 이것으로 대회 결과에 유의미한 영향이 있었다고 생각하지는 않지만, 주최 측에서 부분 점수 풀이를 가를 수 있는 과학적인 기준을 제시하는 데 실패한 것은 유감이다.
10점 전략
가장 단순한 10점 전략은 앞에서부터 순서대로 점을 덮는 것이다. (0, 0)에서 $X$ 좌표가 증가하는 방향으로 잇는데, 해당 $x$ 좌표에 점이 존재한다면 위로 올라가서 해당 점을 덮은 후 $(x, 10^9)$ 에서 다시 오른쪽 방향으로 이어준다. 이후 또 점이 존재한다면 아래로 내려가서 다시 $(x, 0)$ 에서 오른쪽으로 가며, 이렇게 위쪽과 아래쪽을 오가는 것을 반복한다. 이렇게 할 경우 각 점이 유도하는 꺾인 점의 개수가 정확히 2개이기 때문에, $2n$ 개의 선분을 사용하여 대략 10점 정도의 점수를 얻을 수 있다.
50점 전략
위 전략은 한 점에서 다른 점으로 움직이는 과정에서 하나의 선분을 낭비한다. 어차피 각 선분에 2개 이상의 점이 포함될 수 없으니 ($x, y$ 좌표가 모두 다 다름) 결국 대부분의 선분이 하나의 점을 가지고 있는 상황이 이상적일 것이다. 이를 위해서는 선분을 다른 방향으로 돌릴 때도 점을 낭비하지 않도록 신중하게 판단해야 한다.
다음과 같은 "나선" 을 그리는 아이디어를 생각할 수 있다: 초기 (0, 0)에서 시작해서, $x$ 좌표가 최대인 점을 세로로 지나고, $y$ 좌표가 최대인 점을 가로로 지나고, $x$ 좌표가 최소인 점을 세로로 지나고, $y$ 좌표가 최소인 점을 가로로 지나고.. 를 반복하여서 결국 시계 반대방향으로 돌면서 하나의 선분에 하나의 점이 배정되게끔 하는 것이다.
이렇게 하면 항상 점 하나를 제거할 수 있으니 $N+3$ 개 정도의 선분으로 모든 점을 쉽게 덮을 수 있다고 생각할 수 있다. 하지만 이는 사실이 아니다. 다음과 같은 입력을 생각해 보자: $(1, 1), (2, 2), \cdots, (n, n)$ . 이 경우 위와 같은 전략을 사용하면 꼭지점에서만 점을 포함하고 대부분의 선분이 낭비됨을 알 수 있다. 더 자세히 실패 원인을 분석하면, $x$좌표 최대인 점을 방문하면서 이미 $y$ 좌표가 너무 높아진 경우가 존재하여, 이후 남은 점중 $y$ 좌표가 최대인 점을 지날 경우 이것이 예상보다 뒤에 있기 때문에 한번 돌아가야만 이 점을 방문할 수 있기 때문이다.
나선 전략에는 이와 같은 문제가 있으나, 실제 단조성이 없는 대부분의 입력 데이터에서는 이러한 것이 큰 문제가 되지 않는다. 단조성이 필요한 입력 데이터가 공식 데이터에는 많은 편이지만, 아무튼 이 때의 낭비를 무시하고 구현할 경우 50점 정도를 받는다.
100점 전략
이 문제는 $N+3$ 개의 선분을 사용해서 항상 해결할 수 있으며, 이 전략은 $O(N\log N)$ 에 구현할 수 있다.
모든 점이 $(1, 1), (2, 2), \ldots, (n, n)$ 의 형태인 경우에는 항상 문제를 해결할 수 있다. 홀수번째 점은 가로 선분으로, 짝수번째 점은 세로 선분으로 덮는 것을 반복하면, 하나의 선분에 하나의 점이 대응되기 때문이다. 고로 우리는 총 두 가지 전략을 가지고 있다:
- 최대인 점이 겹치지 않는 인스턴스에서만 해결할 수 있는 나선 전략 (50점 풀이)
- 최대인 점이 언제나 겹치는 인스턴스에서만 해결할 수 있는 대각선 전략 (위에서 설명한 것)
정확히 두 극단에 있는 인스턴스에 대해서 문제를 해결할 수 있으나, 실제 문제에서 주어지는 입력들은 이 두 인스턴스가 복잡하게 섞여 있는 경우가 많다. 만약 다음과 같은 형태로 입력을 분할하는 것이 가능하다면 참 좋을 것이다.
- 오른쪽 위를 향하는 대각선으로 구성된 점들 (우상단 / 좌하단 점이 겹치는 케이스에 대응)
- 왼쪽 위를 향하는 대각선으로 구성된 점들 (우하단 / 좌상단 점이 겹치는 케이스에 대응)
- 나선 (그 외 모든 케이스에 대응)
이제 모든 점 집합에 대해서 위 세 집합으로 분할하는 것이 가능함을 보인다. 이에 대해서 여러 설명을 들었는데, 내가 들은 설명 중 가장 깔끔하고 구현이 간단한 것은 김홍녕 님의 아이디어였다. 본인의 허락 하에 이 아이디어를 소개한다.
기본적인 틀은 나선을 긋는 아이디어에 기반한다. 우리는 점 집합에 창문 치기 라는 작업을 반복한다: 점 집합이 주어졌을 때, 이 점 집합을 덮는 최소의 축 평행 직사각형을 찾는 것이다. 이렇게 되면 이 "창문" 에 걸친 점은 $x$ 좌표 최소 / 최대, $y$ 좌표 최소 / 최대가 되는 점들일 것이다. 창문에는 최대 4개의 점이 들어감을 알 수 있다. 이제, 창문에 들어간 점의 개수에 따라서, 창문에서 몇 개의 점을 뺄 것이다.
- 창문에 1개의 점이 걸쳐 있다면, 그냥 점이 하나만 있다는 것이다. 아무 대각선에나 넣어준다.
- 창문에 2개의 점이 걸쳐 있다면, 두 점 모두 창문의 꼭지점에 있으며, 서로 대각선에 반대되는 위치에 있다. 위치 구성에 따라서 두 대각선 중 하나에 넣는다.
- 창문에 3개의 점이 걸쳐 있다면, 정확히 하나의 점만이 창문의 꼭지점에 있다. 이 하나의 점을 두 대각선 중 하나에 적당히 넣고 제거한 후 계속한다.
- 창문에 4개의 점이 걸쳐 있다면, 이 4개의 점을 전부 제거해 준다. 이들은 나중에 나선으로 덮는 데 사용할 것이다.
이 과정에서 계속 $x, y$ 좌표가 최대/최소인 점들이 사라지기 때문에, 창문의 크기는 줄어들며, 또한 계속 안쪽으로 수렴한다 는 사실을 알 수 있다. 즉, 창문 치기를 반복했을 때, 다음에 치게 되는 창문은 그 전에 치게 된 창문에 포함되는 위치에 생성된다.
이제 세 집합이 정말 우리가 원하는 모양인지 확인하고, 그리고 이 집합들을 덮는 방법을 생각해 본다.
- 대각선에 들어가는 점은 모두 각자의 방향으로 증가하는 쪽으로 향한다. 창문의 꼭지점의 위치가 계속 안쪽으로 줄어들기 때문에, 이들의 위치 역시 $x, y$ 좌표가 동시에 감소하거나 증가하는 쪽으로 나열되기 때문이다. 고로 위에서 설명한 방법대로 덮어주면 된다.
- 나선을 덮는 데 사용한 점들을 살펴보자. 이들은 서로 겹치지 않으며 안쪽으로 수렴하는 $K$ 개의 창문들로 구성되어 있다. 50점 풀이처럼 창문을 바깥에서부터 타고 나선을 타면 될 것 같다고 착각할 수 있으나 전혀 그렇지 않다. 창문을 쳤다는 게 나선으로 바로 덮을 수 있다는 것을 뜻하지 않는다. 해결 방법은 창문을 안쪽에서부터 타고 나가는 것이다. 가장 안에 있는 창문을 한 바퀴 돈 후, 빠져나오게 되면 그 다음 창문에 수직으로 나선이 닿게 될 것이다. 나선을 시계 방향, 혹은 시계 반대 방향으로 꺾을 수 있는데, 둘 중 하나는 낭비 없이 모든 점을 방문할 수 있게 창문을 돌 수 있다. 고로 이 두 경우를 나눠서 계속 반복적으로 안에서 밖으로 창문들을 처리해 주면 된다.
고로, 위 세 집합으로 분할하는 것이 가능하다. 이 알고리즘은 점을 $x$ 좌표 증가/감소, $y$ 좌표 증가/감소의 4개 순서로 정렬하고 앞에서부터 차례대로 scan하면 $O(N \log N)$ 에 구현할 수 있다. Output only라서 $O(N^2)$ 정도의 알고리즘을 구현해도 상관이 없지만, 이 풀이의 경우에는 $O(N^2)$ 에 구현하더라도 특별히 쉬워지는 부분은 없다.
각 세 집합을 덮는 방법을 알았으니, 이제 이들을 3개의 추가 선분만을 사용해서 덮는 것이 필요하다. 사실 이 부분이 귀찮다면 대회 시간에는 4개 이상의 추가 선분을 이용해서 덮어도 큰 상관이 없다고 생각한다. 3개의 추가 선분만을 사용해서 덮는 것은 여러 방법이 있을 것이라고 생각한다. 방법 중 하나는 증가 나선 -> 감소 나선 -> 달팽이 형태로 시작해서, 달팽이와 나선 간에 1개의 선분, 나선과 나선 간에 1개의 선분, 증가 나선 앞에서 (0, 0)을 잇기 위한 낭비되는 선분 하나로, 총 3개를 사용하는 것이다. 각 선분을 어떠한 방향으로 이었는지가 매우 중요하고, 또한 각 나선이나 달팽이가 비어 있는 경우 등이 있으니 신중하게 구현하자. Output only라서 corner case 걱정을 덜 해도 되는 것이 약간 다행이지만, 큰 도움이 되는 것 같지는 않다. 구현 관련해서는 Github에 올라온 나의 코드를 보는 것도 좋다.
Problem 5. Vision Program
$W \times H$ 격자가 있고, 각 격자에는 0 혹은 1이 적혀 있다. 이 격자에는 1이 정확히 2개 적혀 있는데, 당신은 두 1의 Manhattan distance가 정확히 $K$ 인지 아닌지를 판단하는 프로그램을 작성해야 한다.
물론 이렇게 하면 문제가 너무 쉬우니, 당신은 이 프로그램을 특정한 프로그래밍 언어를 사용해서 작성하여야 한다. 프로그래밍 언어는 초기 $W \times H$ 개의 Boolean constant에 접근할 수 있으며, 이들은 $0 \ldots WH-1$ 까지의 번호가 붙어 있다. 당신은 이 언어에서 4개의 구문을 사용할 수 있다:
-
AND $X_1 \ldots X_k$ : 새로운 Boolean constant를 만드는데, 이 변수에는 $X_1 \ldots X_k$ 의 Boolean AND 값이 저장되어 있다.
-
OR $X_1 \ldots X_k$ : 새로운 Boolean constant를 만드는데, 이 변수에는 $X_1 \ldots X_k$ 의 Boolean OR 값이 저장되어 있다.
-
XOR $X_1 \ldots X_k$ : 새로운 Boolean constant를 만드는데, 이 변수에는 $X_1 \ldots X_k$ 의 Boolean XOR 값이 저장되어 있다.
-
NOT $X_1$: 새로운 Boolean constant를 만드는데, 이 변수에는 $X_1$ 의 Boolean NOT 값이 저장되어 있다.
새로운 Boolean constant는 만들어진 순서대로 $WH \ldots$ 이상의 번호가 순서대로 붙으며, 그 다음 연산에서 접근 가능하다. 당신의 프로그램은 가장 마지막에 만들어진 Boolean constant에 답을 저장해야 하는데, 만약 거리가 $K$ 이면 답은 1, 아니면 답은 0이어야 한다. 또한, 새로 만든 Boolean constant는 최대 10000개 여야 하며, 각 Boolean constant가 참조한 constant의 개수의 합은 1000000개 이하여야 한다.
Solution
Subtask 1/2/5/6 (41점)
문제가 복잡하게 생겼고, 접근하기 조차도 어려울 것 같아서 겁을 먹기 쉽지만, 사실 단순한 알고리즘을 생각해보면 그렇게 어려운 문제가 아니라는 것을 알 수 있다. 각 점에 대해서 해당 점과 거리 $K$ 인 점들을 고려하고, 두 점 쌍이 모두 1 이면 답이 참이 되게끔 프로그램을 설계하자. 즉, 해당 점, 그리고 해당 점과 거리 $K$ 인 어떤 점의 값을 AND하였을 때 1인 것이 있다면 (OR) 답은 참이다. 이 전략은 (확인이 필요한 쌍의 개수) + 1 개의 상수를 새로 만들게 되는데:
- $max(W, H) \leq 10$ 인 경우에는 이 값이 2000개를 넘지 않는다.
- $min(W, H) = 1$ 인 경우에는 이 값이 400개를 넘지 않는다.
- 점 (0, 0) 이 1인 경우 그 "해당 점" 이 하나밖에 없으니, 그 점에 대해서만 쌍을 만들어주면 이 값이 400개를 넘지 않는다.
이 점을 감안하여 구현하면 41점을 받을 수 있다.
Subtask 3 (52점)
각 점 $p$ 에 대해서 해당 점과 거리 $K$ 인 점 $q_1, q_2, \ldots q_k$ 를 모두 고려해 준 수식의 결과는 다음과 같다.
$(p \land q_1) \lor (p \land q_2) \lor \ldots (p \land q_k)$
이것을 분배법칙으로 묶어주면:
$p \land (q_1 \lor q_2 \lor \ldots)$
이렇게 되면 새로 도입하는 식의 개수가 각 변수마다 겨우 2개밖에 되지 않아서 52점을 받을 수 있다.
100점 풀이
먼저 첫 번째로 맨하탄 거리계를 돌리는 아이디어를 생각할 수 있다. 맨하탄 거리 좌표계는 45도 회전하였을 때 쳬비셰프 거리 (Chebyshev distance) 가 됨이 잘 알려져 있다. 이 경우 같은 거리를 가지는 셀들의 집합이 다이아몬드에서 정사각형의 형태로 바뀐다. 일반적으로 다이아몬드보다는 정사각형의 형태가 직관적인 경우가 많고 이러한 식의 접근은 이 문제에서도 유리하다.
두 번째로, 맨하탄 거리가 정확히 $K$ 가 아니라, 맨하탄 거리가 $K$ 이상 인지를 판별하는 루틴을 구현하는 것을 생각해 볼 수 있다. 만약 우리가 맨하탄 거리가 $K$ 이상인지를 해결하는 루틴을 설계할 수 있다면, $K$ 에 대한 루틴과 $K+1$ 에 대한 루틴을 동시에 구현한 후, 두 루틴의 출력값이 다를 경우 답이 $K$ 이고, 같을 경우 답이 $K$ 가 아니라고 결론내릴 수 있다. 즉, 답이 $K$ 인지를 판별하기 위해서는, 답이 $K$ 이상인지, $K+1$ 이상인지를 판별한 후 이 두 값의 XOR을 취해주면 된다.
$K$ 이상으로 문제를 변환하였을 경우, 문제의 조건이 아주 예쁘게 분리되는 것을 확인할 수 있다. 앞서 소개한 축변환을 사용하면, 두 점의 맨하탄 거리가 $K$ 이상이라는 것은, 두 점의 $x - y$ 좌표 차이가 $K$ 이상이거나, $x+y$ 좌표 차이가 $K$ 이상임을 뜻한다. $x - y = p, x + y = q$ 라고 하면 이는 다음과 같이 쓸 수 있다.
$max(|p_1 - p_2|, |q_1 - q_2|) \geq K$
이 때 max 항을 풀어보면:
$|p_1 - p_2| \geq K \lor |q_1 - q_2| \geq K$
고로, 우리는 $|p_1 - p_2| \geq K$ 인 점 쌍중 두 변수가 모두 1인 쌍이 존재하는지, $|q_1 - q_2| \geq K$ 인 점 쌍중 두 변수가 모두 1인 쌍이 존재하는 지를 또 개별적으로 판별한 후, 이 두 결과를 OR 로 합쳐주면 된다. 일반성을 잃지 않고 이를 $p (x - y)$ 에 대해서만 풀어주자. $q$ 에 대해서는 이와 똑같은 방식으로 해결하면 된다.
$-(m-1) \le i \le n - 1$ 에 대해서 변수 $P_i$ 를, $x - y = i$ 인 셀 중 1인 변수가 하나라도 존재하면 참, 아니면 거짓으로 정의하자. 이러한 변수를 구하는 건 단순히 $x - y = i$ 인 셀들에 대한 값을 OR로 구해주면 되기 때문에 단순하게 구성할 수 있다. 이제 인덱스의 차이가 $K$ 이상이며 모두 1인 두 셀 $P_i, P_j$ 가 존재하면 답이 참이 된다. 이는 모든 $i$ 에 대해서, $j \le i - K$ 인 모든 $j$ 에 대해 $P_i \land P_j$ 가 참이면 답을 1로 만들어 주면 된다. 이렇게 하면 $O((N+M)^2)$ 정도의 풀이를 유도할 수 있고, 상수가 크지만 대략 앞에서 유도한 풀이와 비슷한 점수를 받을 수 있다.
이를 $O(N+M)$ 개의 변수로 줄이는 것은 prefix/suffix OR을 관리하는 일반적인 테크닉으로 해결할 수 있다. 식을 다시 한번 정리해 보자:
$\bigvee_{-(m-1) \le i \le n-1, j \leq i - K}{(P_i \land P_j)}$
$\bigvee_{-(m-1) \le i \le n-1} \bigvee_{j \leq i - K}{(P_i \land P_j)}$
$\bigvee_{-(m-1) \le i \le n-1} P_i \land (\bigvee_{j \leq i - K}{P_j})$
$PFX_i = \bigvee_{j \le i}P_j$ 라고 추가적인 변수를 하나 더 정의하자.
$\bigvee_{-(m-1) \le i \le n-1} P_i \land PFX_{i - K}$
이렇게 할 경우 변수의 개수는 $O(N+M)$ 개, 상태 전이의 개수는 $O((N+M)^2)$ 라서 만점을 받을 수 있다.
첨언
모든 $i \geq -m+2$ 에 대해서, $PFX_i = PFX_{i-1} \lor P_i$ 라는 점화식이 만족하기 때문에 이렇게 할 경우 상태 전이의 개수는 $O((N+M)^2)$ 에서 $O(N+M)$ 으로 줄어든다. 이 문제에서는 제한이 널널하고, 어차피 셀의 개수가 $O(NM)$ 개이기 때문에 필요하지 않은 최적화이다.
이러한 식으로 변수의 개수와 상태 전이의 크기를 줄이는 테크닉은 이전에도 여러 프로그래밍 대회에 출제된 적이 있다. 주로 2-SAT과 연관된 문제의 변수의 개수를 줄이는 데 자주 사용되는데, 이 경우에는 단순히 Prefix의 변수 크기를 줄이는 것 뿐만 아니라, 위에서 언급한 점화식대로 상태 전이의 개수 역시 최적화해야 하는 경우가 많다. 이러한 테크닉을 사용하는 문제로는 다음과 같은 문제들이 있다:
Problem 6. Skywalking
평면 상에 $N$ 개의 가로 선분과 $M$ 개의 세로 선분이 다음과 같은 형태로 주어진다:
- 세로 선분들은 길이 $N$ 의 배열 $x, h$ 로 표현되며, $(x[i], 0)$ 과 $(x[i], h[i])$ 를 잇는다. 이 때 $h[i] > 0, x[i] < x[i+1]$ 을 만족한다.
- 가로 선분들은 길이 $M$ 의 배열 $l, r, y$ 로 표현되며, $(x[l[i]], y[i])$ 와 $(x[r[i]], y[i])$ 를 잇는다. 이 때 $0 \le l[i] < r[i] \le n - 1, 1 \le y[i] \le min(h[l[i]], h[r[i]])$ 를 만족한다. 두 세로 선분은 끝점에서 만날 수 있지만, 그 외 점에서 만날 수 없다.
선분을 벗어나지 않고 움직이면서 $(x[s], 0)$ 에서 $(x[t], 0)$ 으로 가는 최단 경로가 존재한다면 그 길이를 계산하고, 없다면 -1을 반환하라.
Solution
Subtask 1 (10점)
두 선분이 교차하는 위치에 일일이 점을 만들어줘도 그래프가 아주 크지 않다. 고로 $O(|E| \log |E|)$ 에 동작하는 Dijkstra's algorithm 으로 최단 경로를 구하는 식의 풀이를 사용하면 된다. 교점들을 모두 $O(NM$) 시간에 일일이 계산하자. 가로 선분에 대해서 해당 선분이 포함하는 교점의 위치를 전부 나열한 후 (정렬 후 이진 탐색으로 가능) 이들 교점 간에 간선을 이어준다. 세로 선분에 대해서도 동일하게 진행한다. 이렇게 만든 그래프에서 최단 경로 알고리즘을 사용하면 된다. 중복된 교점이 만들어지지 않게 조심하라 (std::unique 를 사용)
Subtask 2 (24점)
교점을 $O(NM)$ 시간에 계산하지 않아야 하는데, 이는 Line sweeping을 사용하면 가능하다. $x$ 좌표가 증가하는 순으로 교점을 찾고, 현재 보고 있는 빌딩을 위 아래로 지나가는 모든 가로 선분을 std::set 과 같은 자료구조로 관리하자. 크게 3가지 이벤트를 처리해야 하는데, 가로 선분 추가, 가로 선분 제거, 그리고 현재 빌딩과 교차하는 가로 선분의 열거가 필요하다. 첫 두개는 자명하고, 마지막은 std::set이 y축으로 정렬되어 있다면 단순히 앞에서부터 순회하면서 교차하는 것에 대해서만 이어주고 나머지는 무시해 주면 된다.
Subtask 4 (57점)
Lemma가 직관적인 편이라 풀이를 짐작하는 것은 쉽지만, 이를 엄밀하게 증명하는 것은 ~해도 해도 문제가 생기는 기하의 묘미~ 상당히 까다롭다. 이 글에서는 완벽히 엄밀한 증명은 아니지만, 그래도 최대한 짧고 납득 가능한 증명을 시도한다.
$s = 0, t = n - 1$ 일 경우 첫번째로 관찰할 수 있는 것은 최단 경로의 $x$ 좌표가 감소하지 않는다는 ($x$-monotone) 것이다. 예제를 보면 알겠지만 이는 일반적인 경우 성립하는 명제가 아니고, $s = 0, t = n - 1$ 인 이 subtask에만 성립한다. 이를 증명하기 위해서는 다음과 같은 사실을 관찰해야 한다:
- 경로는 평면 상에서 교차하지 않는다. (최단 경로니 자명)
- 경로가 ㄹ자나 S자 형태로 굽어 있다면, 이를 $x$-monotone 하게 펼 수 있다.
두 번째 사실에 대해서 첨언하면, 대략 아래 그림과 같이 펼 수 있다:
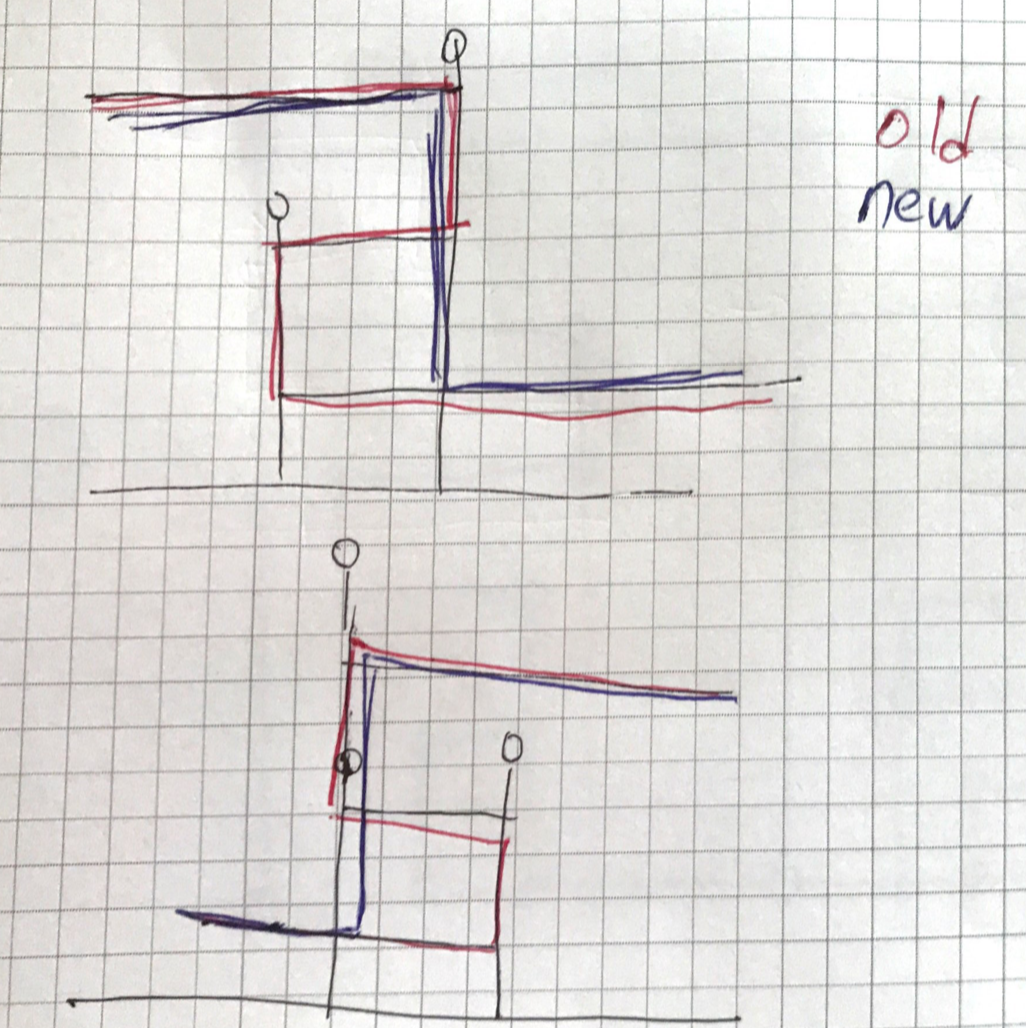
하지만 여기까지 관찰하여도 문제를 해결하기에는 충분치 않다. $x$-monotone한 상황에서 다른 알고리즘 (예를 들어 동적 계획법) 을 고안하더라도 여전히 간선과 정점이 많으며 이들을 효율적으로 처리하는 좋은 방법이 생기지 않기 때문이다. 이제는 다음과 같은 Lemma가 필요하다.
Lemma 1. 어떠한 가로 선분 $S$ 에서 세로 선분 하나를 이용하여 또 다른 가로 선분 $T$ 로 이동할 때, 이 세로 선분의 위치는 $S, T$ 의 양 끝점 중 하나라고 가정할 수 있다.
-
Proof. 어떠한 최단 경로에서 사용하는 가로 선분의 수열을 $[H_1, H_2, \ldots, H_k]$ 라고 하자. 이 때 가로 선분의 수열에 저장된 선분들은, 만약 최단 경로가 원래 가로 선분을 전부 사용하지 않는다면, 원래 주어진 가로 선분들의 부분일 것이다. 가로 선분의 높이가 감소하는 순서대로 정렬하여서 수열을 처리하며, 각 단계에서 우리는 $H_i$ 가 $j < i$ 인 어떠한 다른 가로 선분 $H_j$ 의 양 끝점에서 끝나거나, 아니면 자신의 원래 양 끝점에서 끝나게 변형한다.
$H_1$ 부터 고려하자. 만약 $H_1$ 의 시작/끝점이 원래 $H_1$ 의 시작점과 끝점이 아니라면, 이를 단순히 양 옆으로 늘려주고, 해당 끝에서 아래로 세로 선분을 타고 내려가게 변형해도 거리가 줄어들지 않는다 (어떠한 경로를 최단 경로로 변형했기 때문). 이렇게 되면 $H_1$ 이 사용되는 구간은 전체 구간이 되며, 다른 선분들은 원래 사용되던 구간들이 줄어들거나 아예 사라졌을 가능성이 존재한다. 이제 $H_2, \cdots, H_i$ 에 대해서 다음과 같은 알고리즘을 적용한다:
- $H_i$ 전부가 다른 $H_j$ 들에 의해서 덮여 사라졌거나, 양 끝점이 다른 $H_j (j < i) $ 에 의해 모두 좁아졌다면 증명 종료.
- 일반성을 잃지 않고 $H_i$ 의 현재 시작점이 원래 시작점과 다르며, 시작점이 다른 $H_j (j < i)$ 에 의해 좁혀지지 않았다고 하자. 시작점을 원래 시작점 방향으로 계속 왼쪽으로 밀어준다. 이 과정에서 다른 $H_j (j < i)$ 를 만났다면 그 위치에서 정지하고 최단 경로를 늘려준 구간으로 변형한다. 그렇지 않고 시작점까지 갔다면 시작점에서 정지한후 앞과 같이 시작점에 닿는 세로 선분을 타고 내려가도록 한다. 이 과정에서 중간 경로는 모두 최단 경로로 대체되었으니 길이가 줄지 않았다.
이제 동적 계획법을 사용할 수 있다. 일반성을 잃지 않고 가로 선분은 길이가 0이라고 하자 (나중에 답에 $X[n-1] - X[0]$ 을 더해주면 된다). $DP[i][j]$ = $(x[i], j)$ 위치로 오는 최단 경로 라고 정의하자. 이 때 $j$ 의 범위가 너무 클 수 있으니, 의미있는 위치에 대해서만 (어떠한 선분의 높이 $y[i]$ 와 일치하는 $j$ 에 대해서만) 상태를 관리해 줘야 한다.
이제 상태전이는 다음과 같다.
- 만약 $(x[i], j)$ 가 어떠한 가로 선분의 시작점이면, $DP[i][j] = min_{0 \le k \le y[i]}(DP[i-1][k] + |j-k|)$ (시작점에 값 지정)
- 만약 $(x[i], j)$ 가 어떠한 가로 선분의 끝점이면, 모든 $0 \le k \le y[i]$ 에 대해 $DP[i][k] \leftarrow min(DP[i][k], DP[i-1][j] + |j-k|)$ (끝점에서 나오는 값 뿌려주기)
- 그 외 모든 경우에 대해 $DP[i][k] = DP[i-1][k]$
이러한 연산을 단순하게 하면 $O(NM)$ 시간이 들지만, Lazy propagation을 동반한 Segment Tree를 사용하여 $DP[i][j] - j, DP[i][j] + j$ 의 최솟값을 관리하면 각 시작점과 끝점에 대해서 $O(\log M)$ 에 모든 처리가 되기 때문에 $O((N + M) \log M)$ 시간에 문제가 해결된다.
이 풀이를 훨씬 더 간단하게 변형할 수도 있는데, 이에는 다음과 같은 Lemma가 필요하다.
Definition. 어떠한 끝점 $(x[i], j)$ 에 아래로 인접한 선분을, $l[k] \le x[i] \le r[k]$ 를 만족하며, $y[k] < j$ 를 만족하는 선분 중 $y[k]$ 가 가장 큰 것으로 정의하고, 위로 인접 한 선분은 $y[k] > j$ 에 대해 동일하게 정의하며, 이 둘을 합쳐 인접 한 선분이라 하자.
Lemma 2. 시작점과 끝점에 대한 상태 전이를 할 때, 모든 선분에 대해서 할 필요가 없이, 인접한 두 선분에서만 값을 받고 뿌려주면 된다.
Proof. Lemma 1과 비슷한 증명법을 사용한다. 어떠한 최단 경로를 높이가 감소하는 순으로 처리하면서, 위 Lemma를 만족하게끔 변형할 것이다. 이는 다음과 같이 진행된다:
- 현재 높이에서 덮이지 않은 (이보다 더 높은 위치에서 통과하지 않은) $x$좌표 구간들을 고려하자. 각 처리 과정에서 이들 구간들을 최소한으로 좁혀준다 - 현재 높이에서, 해당 구간의 시작점이나 끝점을 지나는 가로 구간들이 있으면, 해당 구간을 타고 최대한 많은 $x$ 구간을 덮어주며, 전부 덮는 것에 실패하였다면 거기서 아래 방향으로 세로 선분을 타고 빠져나가게 하자. 이를 반복하면, 모든 이동이 아래로 인접 / 위로 인접한 선분을 타고 가는 것으로 표현된다.
이제 위 상태 전이에서 전체 구간을 고려할 필요가 없이 양 옆으로 인접한 구간만 고려하면 되기 때문에, Segment tree를 사용할 필요가 없고, Subtask 2와 거의 동일한 풀이를 사용할 수 있다. 똑같이 Line sweeping을 진행하는데, 각 가로 선분에 대해서, 해당 선분의 끝점, 그리고 끝점에 인접한 두 양 선분에 대해서만 교점을 만들어준다. 이렇게 할 경우 $N + 6M$ 개의 교점이 나오며, 이들을 Subtask 2와 동일하게 처리해 주면 문제를 해결할 수 있다.
100점 풀이
$s = 0, t = n - 1$ 조건이 없으면 온갖 못 생긴 상황을 다 감수해야 한다. 일반성을 잃지 않고 $s < t$ 라 하자. 예를 들어:
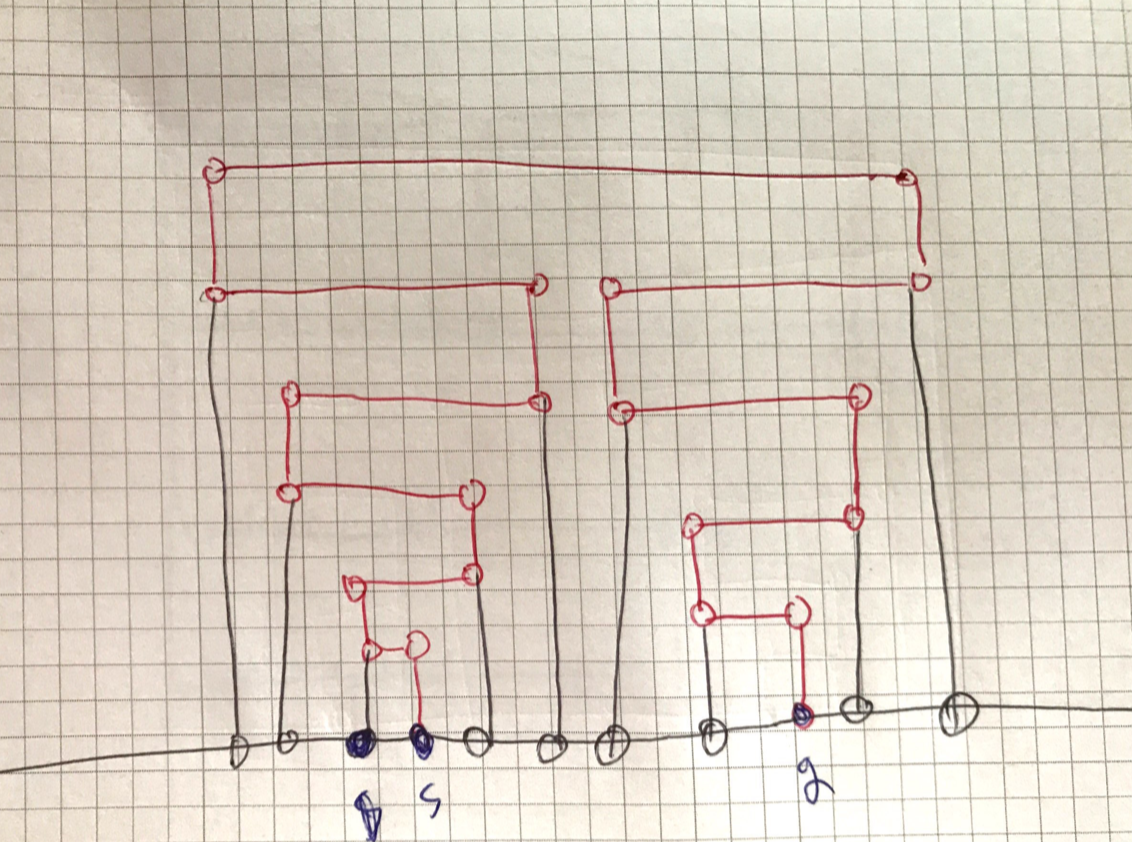
이 경우 $s$ 에서 $t$ 로 가는 유일한 경로가 저런 모양으로 생겼다. 이러한 상황이 생기는 이유는 기본적으로 앞의 ㄹ자 형태를 풀어주는 argument가 먹히지 않아서고, 먹히지 않는 이유는 세로 선분에 높이 제한이 있기 때문이다. 만약 Subtask 3과 같이 모든 세로 선분의 높이가 동일하다면 ㄹ자 argument가 통해서 단조성이 성립하기 때문에 $s, t$ 가 $0, n-1$ 이 아니어도 57점 풀이와 같은 방식으로 문제를 해결해 줄 수 있다. 단순히 $s, t$ 왼쪽에 있는 선분들을 모두 무시해주면 되기 때문이다.
한편 이 반례를 그려보면 상당히 그럴듯한 해결책을 찾을 수 있다. 경로는 어떠한 시작점 $s$ 에서 가장 왼쪽 세로 선분인 $l$ ($l \le s$)을 거치고, 그 이후 가장 오른쪽 세로 선분인 $r$ ($r \geq t$) 를 거친 후, 끝점 $t$ 로 갈 것이며, $l \rightarrow r$ 로 가는 경로 자체는 57점 풀이와 똑같은 이유로 단조성이 성립한다. 결국 $s, t$ 근처에서 $l \rightarrow r$ 로 가는 경로를 진입하기 위해서 위와 같은 형태로 올라가는 것인데, 그렇다면 각 가로 선분에 대해서 $s, t$ 에 가장 가까운 점을 각각 2개, 총 $4M$ 개의 점을 추가하고, 이 점에 대해서 위 아래로 인접 한 점을 만들어주면, 위로 올라가는 길이 뚫린다고 생각할 수 있다. $4M$ 개의 점을 찾는 것은, 높이 순으로 정렬한 후 $x$ 축으로 정렬된 세로 선분들의 std::set을 가지고 있다면 스위핑 과정에서 lower_bound 및 upper_bound 연산으로 간단하게 찾을 수 있다. 이렇게 되면 그래프에는 총 $N + 18M$ 개의 정점이 생기고, 이 그래프에서 실제로 최단 경로를 구해주면 정답을 받을 수 있다. 이 때의 시간 복잡도는 $O((N + M) \log (N + M))$ 이다. 이제 이를 증명하려고 시도한다.
Lemma 3. 어떠한 가로 선분 $S$ 에서 세로 선분 하나를 이용하여 또 다른 가로 선분 $T$ 로 이동할 때, 이 세로 선분의 위치는 $S, T$ 의 $s$ 에 가장 가까운 양 끝점 중 하나라고 가정할 수 있다.
Proof. 사용되는 모든 가로 선분을 방문 순서대로 나열하고, 수학적 귀납법을 사용하자. 맨 첫 원소는 자명하게도 한쪽 끝점이 가장 가까운 앙 끝점 중 하나에 있다. 이제 두번째 원소부터 시작하자. 6가지 케이스가 있다.
- $S$ 가 $s$ 를 관통하며, $T$ 가 $S$ 에서 움직이는 것과 같은 방향으로 움직임
- $S$ 가 $s$ 를 관통하며, $T$ 가 $S$ 에서 움직이는 것과 반대 방향으로 움직임
- $S$ 가 $s$ 를 관통하지 않고 $s$ 에서 멀어지는 방향이며, $T$ 가 $S$ 에서 움직이는 것과 같은 방향으로 움직임
- $S$ 가 $s$ 를 관통하지 않고 $s$ 에서 멀어지는 방향이며, $T$ 가 $S$ 에서 움직이는 것과 반대 방향으로 움직임
- $S$ 가 $s$ 를 관통하지 않고 $s$ 로 가까워지는 방향이며, $T$ 가 $S$ 에서 움직이는 것과 같은 방향으로 움직임
- $S$ 가 $s$ 를 관통하지 않고 $s$ 로 가까워지는 방향이며, $T$ 가 $S$ 에서 움직이는 것과 반대 방향으로 움직임
모든 케이스에서 다음과 같은 전략을 사용하자: 만약 모순이 생겼다면, 해당 $T$ 에서 $s$ 에 조금 더 가까운 교점을 기준으로 선을 잇는다. 이 경우 이렇게 이은 선은 기존 최단 경로와 교차하는 지점이 존재한다. 이 지점에서 최단 경로를 교체해 주면 거리가 줄어들고 모순을 해결할 수 있다. 실제 확인은 손으로 잘 해보길 바란다.
Lemma 4. $s \rightarrow l$ 로 가는 최단 경로에서 사용한 세로 선분의 $x$ 좌표 수열을 $[SQ_1, SQ_2, \cdots, SQ_k]$ 라고 하자. 모든 $i$ 에 대해서 $SQ_i$ 는 $[SQ_1, \cdots, SQ_i]$ 의 최댓값이거나, 최솟값이다.
Proof. 그렇지 않은 $i$ 가 존재하면 해당 시점에서 값을 줄일 수 있다.
Lemma 5. 상태 전이를 할 때 모든 선분에 대해서 할 필요가 없이, 인접한 두 선분에서만 값을 받고 뿌려주면 된다.
Proof outline. Lemma 4에서 사용한 $x$ 좌표 수열을 거꾸로 보면서 이를 "블록" 으로 분해한다. 각 블록은, $SQ_i > s$ 혹은 그 반대를 만족하는 maximal한 부분 수열이다. 이 부분 수열의 경로를 최대한 위쪽 으로 대체하자. 즉, 같은 거리를 유지하면서 위쪽으로 경로를 올릴 수 있다면 그렇게 하는 것이다. 이는 다음과 같이 할 수 있다. 경로를 아래로 타고 내려가면서 다음과 같은 대체 가 존재하는 지 확인하자:
- 현재 경로에서 $s$ 에 가까운 쪽으로 움직이고, $s$ 에 도달하기 직전에 세로 선분으로 탈출해서 다시 원래 최단 경로로 복귀 가능한 경로
이를 반복하다 보면 각 블록이 실제로 이루는 경로가 $s$ 에 가까워지는 방식으로 계속 좁아짐을 관찰할 수 있고, 이 과정에서 Lemma 4 역시 깨지지 않는다는 것을 알 수 있으며, 또한 모든 이동이 만들어 준 정점에서만 일어나도록 변형됨을 알 수 있다. 고로 주어진 $N + 18M$ 개의 정점에 대해서만 문제를 해결해주면 된다.
첨언
이 문제의 경우, 세로 선분에 대해서는 (일반성을 잃지 않고) 거의 제약 조건이 없으나, 가로 선분이 $y = 0$ 이라는 핵심적 제약 조건이 있어서 문제가 해결된다. 이 조건이 없더라도 $N$ 개의 축 평행 선분에 대해서 $(N + Q) poly(\log N)$ 에 문제를 해결할 수 있다고 들었다. 관심있는 독자는 시도해 보길.
'공부 > Problem solving' 카테고리의 다른 글
| 장애물을 포함하지 않는 가장 큰 직사각형 찾기 (15) | 2019.10.21 |
|---|---|
| 2019.09.13 problem solving (3) | 2019.09.12 |
| IOI 2019 Day 1 (2) | 2019.08.14 |
| 2019 한국정보올림피아드(KOI) 고등부 문제 풀이 (9) | 2019.07.22 |
| 2019 한국정보올림피아드(KOI) 중등부 문제 풀이 (0) | 2019.07.22 |
- Total
- Today
- Yesterday
