티스토리 뷰
A deterministic near-linear time algorithm for finding minimum cuts in planar graphs
구사과 2023. 11. 23. 07:49https://dl.acm.org/doi/pdf/10.5555/982792.982916
Cut-cycle duality에 의해 $G$ 에서 minimum cut을 찾는 것은 $G^*$ 에서 minimum cycle을 찾는 것과 동일하다.
아이디어는, $G^*$ 에서 적당한 사이클 $C$를 찾은 다음, $C$의 *안* 과 *밖* 에 대해서 분할 정복을 하고, 이후 $C$의 안과 밖을 오가는 사이클을 찾는 것이다.
분할 정복이 성립하려면 일단 $C$가 $G^*$ 의 Face들을 공평하게 쪼개야 할 것이다. 이런 $C$는 $O(n)$ 시간에 찾을 수 있다. $G^*$ 의 모든 Face를 대각선에 $\infty$ 가중치 간선 넣고 대충 triangulate하자.
다음, $G^*$ 에서 아무 정점을 잡고, shortest path tree를 만들자. 이 shortest path tree에는 $\infty$ 가중치 간선이 전혀 없음을 볼 수 있다. shortest path tree를 $T^*$ 라고 하자. primal 에서의 $E \setminus T$는 스패닝 트리이며, dual의 모든 face가 삼각형이기 때문에 Degree가 3 이하이다. 고로 $e$를 제거했을 때 양 컴포넌트가 $2/3n$ 이하인 $e$가 존재한다.
이제 다시 dual로 오자. 이 말은 어떠한 간선 $e^*$가 존재하여, $T^* + e^*$의 fundamental cycle이 양 컴포넌트를 $2/3n$ 이하로 나눈다는 것과 동일하다. $e^*$ 가 triangulation을 위해 만든 dummy 간선일 수 있는데, 그러면 그 dummy 간선이 생긴 face를 기준으로 아래쪽 경로를 타는 것으로 해 주자. 그러니까, $e^*$ 가 속하는 face가 사이클 안에 들어가도록, 그렇게 설정해 주면 된다.
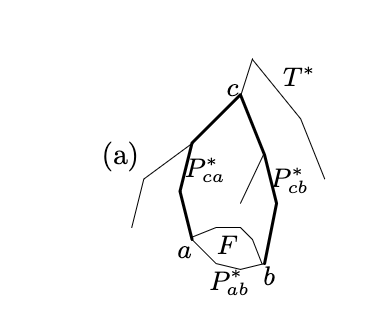
$e^*$ 가 속하는 face가 $F$이고, $P_{ab}^*$ 이 탄 아래쪽 경로이다. $e^*$ 가 더미 간선이 아니더라도 뭐 이런 식으로 그림을 그려줄 수 있겠다.
이제 저 사이클이 Face를 2/3 크기로 나눈다는 것은 알 수 있다. 그러면 재귀적으로 저 사이클 안과 밖에 완전히 포함되는 최적해는 구할 수 있다.
(dummy를 원래 간선으로 바꿔주면서 깨질 수도 있지 않나요? -> triangulation을 consistent하게 해 준다고 생각해 보면 걱정할 필요가 없다.)
(사실 저 사이클의 크기가 열라 크면 분할 정복이 깨질 수도 있다는 생각은 있다. degree 2인 정점을 condense하는 작업이 필요할 수 있다.)
마지막으로 저 사이클을 넘나드는 경우를 해결해야 한다. $c$를 포함하고 사이클 밖에 있는 아무 Face를 잡자.

넘나드는 사이클이 $F$와 $F_a$ 중 정확히 하나만 포함한다면, $s - t$ min cut이고, $O(n \log n)$ 에 구할 수 있다 (메시라이브)
둘 다 포함한다고 생각하면, path $c - a$ 안과 밖을 왔다 갔다 하거나 $c - b$ 안과 밖을 왔다 갔다 해야 한다. 처음 들어온 순간과 나가는 순간을 그냥 shortest path $c - a$로 대체시키면 답이 무조건 그 이상이다. 둘 다 포함하지 않는다고 생각하면 저 사이를 약간 십자가처럼 패싱해야 하는데 동일한 논리가 성립한다.
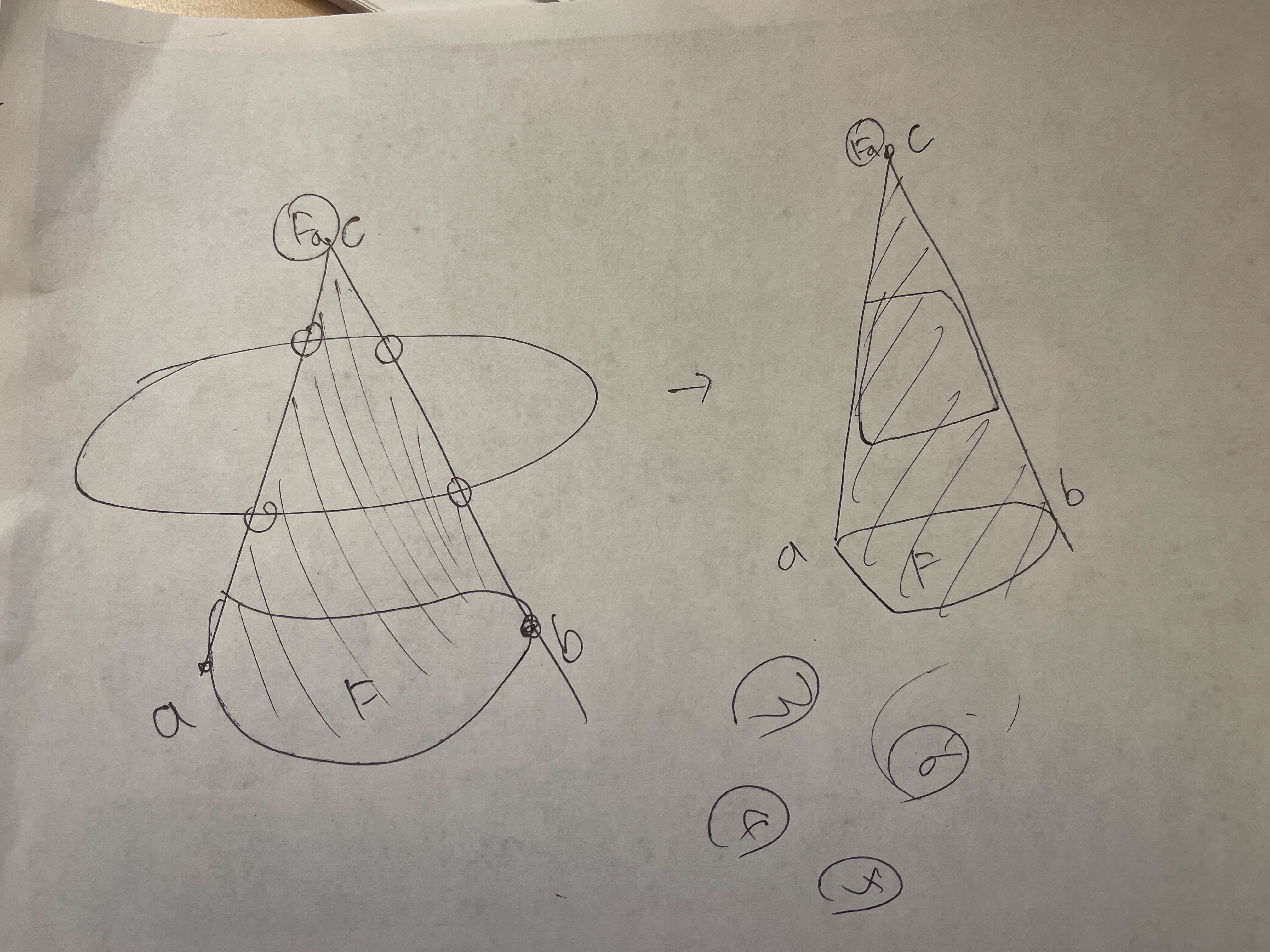
(두 번째 케이스의 사진)
고로 마스터 정리에 의해 전체 문제가 $O(n \log^2 n)$ 에 해결된다. $O(n \log \log n)$ 에 더 빠르게 해결할 수도 있다. https://arxiv.org/pdf/1104.4890.pdf
'공부 > CS theory' 카테고리의 다른 글
| Graph Spanners (0) | 2024.04.14 |
|---|---|
| Randomized algorithms - 2023.12.08 (0) | 2023.12.08 |
| Incremental approximate $s - t$ max flow in $m^{1/2+o(1)}$ update time (0) | 2023.11.18 |
| Introduction to Distributed Graph Algorithms (2) | 2023.06.29 |
| Separating Hyperplanes, Lagrange Multipliers, KKT Conditions, and Convex Duality (0) | 2023.05.18 |
- Total
- Today
- Yesterday
