티스토리 뷰
Result Analysis
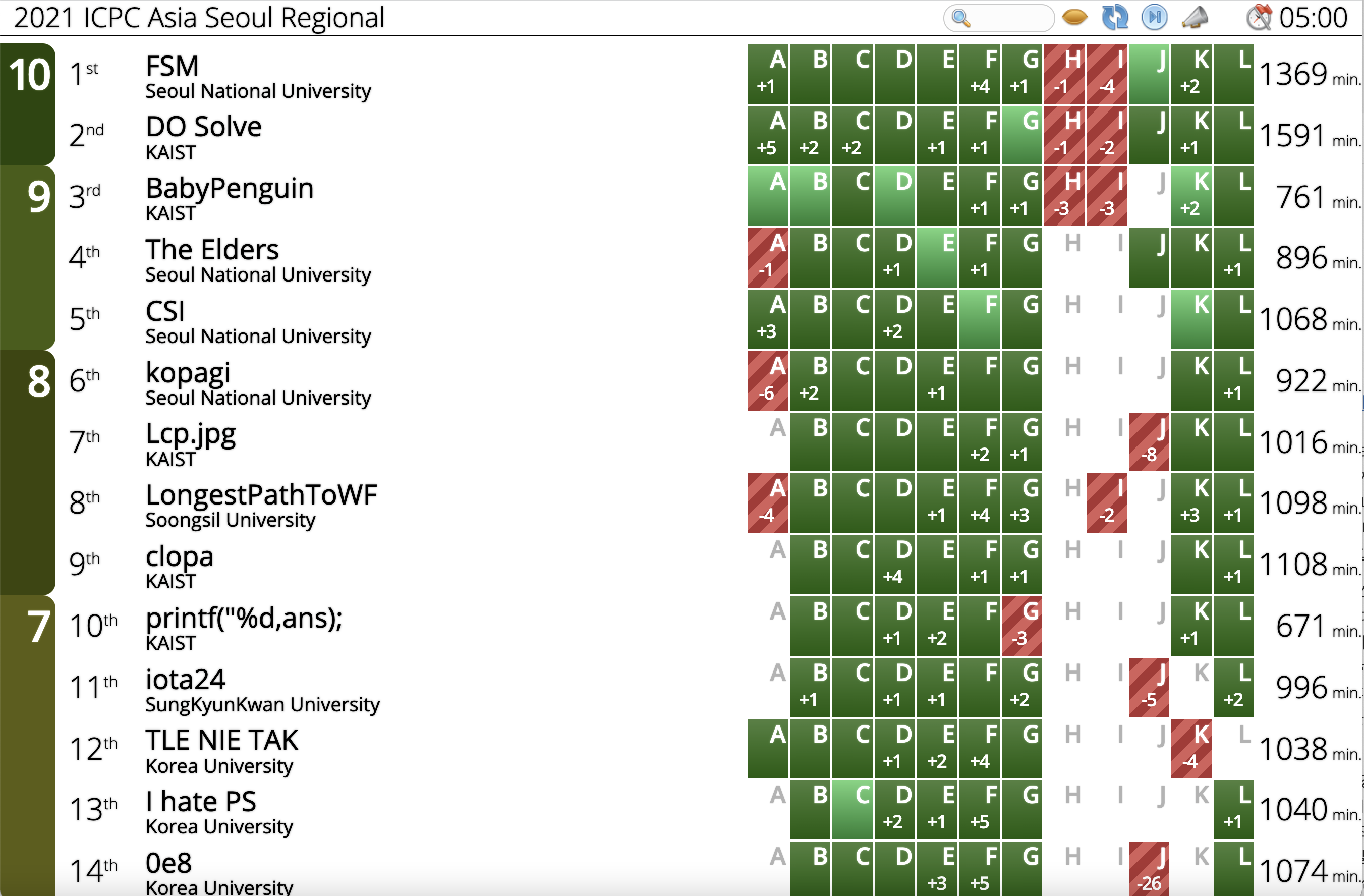
이번 서울 리저널에서의 각 대학 별 상위 팀은 다음과 같다. 별 일 없다면 상위 3팀이 진출할 것이다.
- 서울대학교: FSM (World Finals 진출 확정)
- KAIST: DO Solve (World Finals 진출 확정)
- 숭실대학교: LongestPathToWF (World Finals 진출 매우 유력)
- 성균관대학교: iota24 (World Finals 진출 가능성 약간 존재)
- 고려대학교: TLE NIE TAK
서울대학교의 FSM 팀은 2020년 대회를 우승한 Let Us Win ICPC WF 팀과 동일한 멤버로 출전하였다 (김세빈, 윤교준, 이민제). 2020년에도 신입생 팀으로 ICPC Regional Champion을 차지한 팀으로, UCPC 2021, SCPC 2021 (이민제) 등등 그 사이에도 좋은 활약을 보여주더니 2021년에도 동일한 팀으로 우승하였다. 최소 최근 10년 동안 연속으로 서울 리저널을 우승한 팀은 물론이고, 개인 참가자도 존재하지 않는다. 신입생 3명이 팀을 꾸려서 2년 연속 우승을 했으니 한동안 깨지기 힘든 대기록이 아닐까 싶다. 사실 이 팀은 초중반에 상당히 부진해서 한 10등 근처까지 내려가기도 했다. 이대로 2연 우승은 안 나오나 싶었지만, 분위기를 반전시켜서 결국 The Elders, CSI와 함께 8솔브로 프리즈를 맞이했다. 프리즈 동안은 세 팀의 상태가 비슷해서 예측이 어려웠는데, FSM이 그냥 많이 풀고 이겼다. 축하합니다!
KAIST의 DO Solve 팀은 신입생 팀으로 역시 강력한 멤버들로 구성되어 있다 (김석표, 이온조, 임성재). 카이스트의 내부 경쟁은 전년도에 비해서 매우 치열한 편으로, 사실 올해도 카이스트가 6년 만에 리저널 챔피언을 되찾을 수 있다고 기대했으나 약간 안타까운 느낌이 든다. (내년에는 웬만하면 되찾을 것이라고 생각한다.) DO Solve 팀은 항상 상위권 실력을 꾸준히 보여줬으나, 같은 학교의 BabyPenguin 팀이 최근 여러 활약을 보여주고 있어서 월드 파이널 진출의 기대치가 높은 팀이라고 하기는 어려웠다. 초중반에도 BabyPenguin 팀이 다른 모든 팀들을 2문제 격차로 벌리며 이변이 없음을 보여주었고, 프리즈 직후 1등인 BabyPenguin만이 관심을 독차지하면서 유종의 미 정도로 끝나나 했다. 하지만 프리즈 동안 무려 3문제를 풀어 냈고, 그 중 J를 풀어낸 것이 결정타로 작용해 BabyPenguin을 문제 차로 이겼다. 축하합니다!
숭실대학교의 LongestPathToWF 팀은 2020년에 181920이라는 이름으로 출전했던 팀으로, 올해 멤버 변경 없이 이름만 바꿔 그대로 출전했다 (안용현, 오주원, 이성서). 숭실대학교는 월드 파이널에 진출한 적이 없고 그에 근접했던 적도 최근에 없는데, 2020년에 181920 팀이 월드 파이널 티켓 3슬롯에 거의 근접해서 많은 관심을 끌었다. 당시에도 고려대학교 팀 (그때는 호에엥하와왕 팀으로 올해와 멤버가 다르다) 과 라이벌 관계가 있었고, 실제로 인터넷 예선에서 승리했지만, 결국 본선에서 밀려 월드 파이널에서 탈락했다. 사실상 고려대 팀과 함께 이번 리저널이 가장 중요하고, 그래서 가장 연습을 많이 한 팀 중 하나라고 생각한다. 올해는 반대로 예선에서 패배했으나 본선에서 고려대학교 팀에 설욕하였고, 숭실대 최초로 ICPC World Finals에 진출하였다. 이 팀은 팀연습때 내가 가끔씩 들어가 봤는데, 연습기간 초반부에는 고려대학교 팀을 여유롭게 따돌렸던 것 같은데 후반부 되어서 퍼포먼스가 안 좋아져서 크게 걱정했었다 (이 내용은 팀원들에게 한번도 말한적 없고, 여기서 처음 밝힌다 ㅋㅋ). 다행이도 리저널에서는 제 실력을 발휘한 것 같다. 축하합니다!
Problem Analysis
올해 문제는 예년 비해서 상당히 어렵게 출제된 편이다. 거의 모든 해에서 우승 팀이 모든 문제를 풀었고, 그렇지 않은 해 (2015, 2018 등) 에도 웬만하면 한 문제 빼고 다 풀었다는 점을 감안하면 상당히 이례적이다. 다만 모든 문제를 푸는 난이도는 솔직히 2018년이 더 어렵지 않나 싶다. 솔직히 말해서 문제가 자꾸 봤던 유형에서 계속 재탕 삼탕하는 느낌이 너무 강하다. 어느 정도야 그럴 수 있겠지만 올해는 오리지널한 문제가 많이 없는 것 같다.
A. Ant Colonies
선형일 때 문제를 해결하는 방법은 다음과 같다. 각 색 $i$ 에 대해서, Segment tree를 통해서 구간의 가장 왼쪽 / 오른쪽에 있는 $i$ 번 색 노드의 위치와, 그 사이에 있는 가장 가까운 점 쌍 거리를 계산해 둔다. 이 값을 계산해 두면 두 서브트리의 값을 $O(1)$ 시간에 합칠 수 있다. 다만, Segment tree의 공간 복잡도가 $O(N^2)$ 로 커질 수 있기 때문에 필요한 노드들만 포인터로 만들어주는 식의 최적화가 필요하다. 이 경우 시간 복잡도는 $O(N \log N + Q \log N)$ 이다.
트리일 경우에는, Heavy-light decomposition으로 위와 똑같은 내용을 구현해 주면 된다. 정말 똑같기 때문에 특별히 더할 말이 없다. Heavy light decompostion은 구현 방식에 따라서 코드의 길이가 크게 달라지기 때문에, 선형일 때와 문제가 많이 다른 것 같다면 좋은 구현을 읽어보는 것이 도움이 될 것이다. 예를 들어, 각 체인에 대해서 세그먼트 트리를 두면 공간 복잡도가 $O(N^2)$ 가 되어 최적화가 필요하다. 하지만 세그먼트 트리는 전역에 각 색마다 하나만 두고, 체인마다 정점 인덱스를 따로 배정해 두면 다른 체인이 같은 자료구조를 사용하게 되고, 고로 공간 복잡도를 줄일 필요가 없다.
시간 복잡도는 $O(N \log N + Q \log^2 N)$ 이다.
나는 위 풀이를 다음과 같이 구현하면 간단하다고 생각한다. 쿼리를 오프라인으로 처리한다. HLD까지는 그대로 하는데, 각 노드에 0 혹은 1의 수가 쓰여 있다고 생각하자. 역시 Segment tree를 사용하여, 구간의 가장 왼쪽 / 오른쪽에 있는 1, 그리고 가장 가까운 1 쌍 거리를 관리한다. 색깔이 N개가 아니라 1개이니 $O(N)$ 크기의 세그먼트 트리를 구성할 수 있고 포인터를 사용한 메모리 절약이 필요하지 않다. 업데이트 쿼리를, "어떠한 색 $c$ 가 정점에 적힌다", "어떠한 색 $c$ 가 정점에서 지워진다" 로 쪼개자. 그리고 업데이트 및 경로 쿼리를 색상 별로 묶으면, 같은 자료구조를 돌려쓰면서 위 쿼리를 따로 처리할 수 있다.
B. Double Rainbow
색 $i$ 의 등장 횟수를 $cnt[i]$ 라고 하자. 우리는 모든 수 $1 \le j \le k$ 에 대해 $j$ 의 등장 횟수가 $[1, cnt[j]-1]$ 범위에 속하는 구간을 찾으려고 한다.
$P^\prime$ 의 시작점을 고정시킨 후, 끝점을 증가시키면서 해당 부분 배열에서 모든 수의 등장 횟수를 다른 배열에 관리하자. 만약 등장 횟수가 $cnt[i]$ 를 찍은 숫자 $i$ 가 나왔다면 더 이상 진행할 수 없다. 그 전에 모든 수가 $P^\prime$ 에 등장했다면, 해당 시작점에서 가장 짧은 double rainbow 를 찾은 것이니 답을 갱신한다. 이를 모든 시작점에 대해서 해 주면 $O(n(k + n))$ 에 문제가 해결된다. 더 빠른 (선형 시간) 풀이도 존재한다.
C. Find the House
지문이 조금 복잡하고, 사실 refer 라는 단어로 무슨 말을 하려고 하는지 모르겠다. 정의라도 했으면 좋겠는데 그것도 없다.
refer 가 방문의 의미로 사용되었다고 해석하면, 문제 지문에 Each of the triples in the list is referred exactly once. 라는 문구가 있다.
트리플렛은 중간 과정이 어찌됐든 정확히 한 번 방문할 것이니, 트리플렛이 증가/감소시키는 좌표의 합만 구해주면, 시작 위치에서 해당 값을 더해줌으로써 최종 위치를 알 수 있다.
D. Friendship Graphs
간선의 존재 여부를 뒤집어서, 입력으로 주어지지 않은 $n(n-1)/2 - m$ 의 정점 쌍간에 간선이 있는 그래프를 생각해 보자 (complement graph). 우리는 이 그래프의 정점을 두 부분으로 나눠서, 각 부분에 대해 같은 부분을 잇는 간선이 없는 것이 가능한지를 알고 싶다. 이는 그래프가 이분 그래프인지를 판별하는 것과 동치이다. 고로 이 그래프가 이분 그래프이면 답이 존재한다.
이제 각 그룹의 크기 차를 최소화해야 한다. 그래프가 연결 그래프라면 각 정점이 무슨 집합에 들어가는 지 알 수 있으니 크기 차가 고정되어 있다. 여러 컴포넌트로 이루어져 있다면 각 컴포넌트의 두 정점 집합을 그대로 넣을지, 아니면 색을 뒤집어 넣을지 결정할 수 있다. 이는 일종의 Knapsack의 형태라서, DP를 사용하여 해결할 수 있다.
$dp[i][j] = $ ($i$ 번 컴포넌트까지 고려했으며 $A$ 의 크기가 $j$ 일 수 있는가) 와 같이 DP 점화식을 세우면, $O(N^2)$ 에 테이블을 채울 수 있다. 컴포넌트 개수를 $C$ 라고 하면, $j \le n/2$ 이면서 $dp[C][j]$ 가 참인 최대 $j$ 가 $A$ 의 크기이고, $N - j$ 를 $B$ 의 크기라고 볼 수 있다. 이를 채워주면 $O(N^2)$ 에 전체 문제가 해결된다.
여담으로 아마 이 문제는 $O(M \log N + N \sqrt N)$ 에도 해결할 수 있다.
E. Grid Triangle
생각을 깔끔하게 하기 위해 다음과 같이 간소화해서 생각하면 좋다.
- $0, A, B$ 를 모서리로 한 삼각형과 $0, B, A$ 를 모서리로 한 삼각형을 문제에서는 하나로 보는데, 둘을 다른 삼각형으로 본다. 달리 말해, 삼각형의 영점이 아닌 모서리를 빨간색과 파란색으로 칠했다고 보고, 색이 다르면 다른 삼각형으로 세는 것이다. 이후 구한 답을 2로 나눈다.
- 색칠했다는 가정을 그대로 가져간 후 삼각형의 빨간 모서리가 무조건 $x > 0, y > 0, z > 0$ 영역에 있다고 가정하자. 그 외 경우는 적당히 대칭시켜서 위와 같은 경우로 항상 만들어 줄 수 있으니, 구한 답을 8배하면 된다.
- 삼각형의 빨간 모서리가 $x < y < z$ 를 만족한다고 가정하자. 그 외 경우는 $A, B, C$ 의 모든 순열을 다 해보면서 6개의 케이스를 다 해보자.
모든 조건을 추가했을 때, 빨간 모서리의 위치가 $(x, y, z)$ 라면, $z = x + y$ 를 만족해야 하며, 파란 모서리의 위치는 항상 다음과 같은 두 가지 경우만 가능하다:
- $(-y, z, x)$
- $(z, -x, y)$
이에 대한 증명은 잘 모른다. 본인의 경우 위까지 관찰한 후 규칙이 나올 것이라고 생각하여 컴퓨터로 전수탐색을 하여 규칙을 찾을 수 있었다. 나는 대회여도 이렇게 해 봤을 것 같은데, 팀 성향에 따라 결정하면 될 것 같다.
이제 $(-y, z, x)$ 의 경우를 해 보자. 이제 문제는 $0 < x < y$ 이면서 다음 조건을 만족하는 정수를 세는 문제가 된다.
- $max(y, x) = y \le A$
- $max(x + y, y) = x + y \le B$
- $max(x, x + y) = x + y \le C$
$A$ 의 크기가 작기 때문에, $1 \le y \le A$ 를 전부 해 본 후 $x$ 의 개수를 세면 된다. $x$ 는 $min(y - 1, B - x, C - x)$ 보다 작은 양의 정수이니, 그 개수는 쉽게 알 수 있다. $A$ 의 크기도 작고, 이 연산을 6번 하니, 시간 안에 충분히 돈다. $(z, -x, y)$ 의 경우도 비슷하게 직접 해 볼 수 있다.
F. John's Gift
만약 $n$ 개의 상품과 가격표를 전부 매칭시키는 문제라면, 답을 최적화하는 매칭은 그리디하게 찾을 수 있다. 상품의 가격을 정렬한 것을 $a_1, a_2, \ldots, a_n$, 가격표의 가격을 정렬한 것을 $b_1, b_2, \ldots, b_n$ 이라고 하자. $i$ 번째 상품과 가격표를 매칭하면 되고, 이 때의 답은 $max_{i}|a_i - b_i|$ 로 표현할 수 있다. 즉, 제거할 상품을 고정하고, 제거할 가격표를 고정한 후, 위 답을 매번 재계산하면 $O(n^3)$ 시간에 문제를 해결할 수 있다.
이를 최적화해보자. 최솟값 뿐만 아니라 최솟값을 만드는 최소 크기 상품 역시 알아야 하니, 각 상품에 대해서 답을 모두 구할 수 있으면 편리할 것이다. $i$ 번 상품이 제거되었다면, 그 외 상품들이 매칭되는 경우는
- 가격표 $j \le i$ 가 제거되어 $(1, 1) \ldots (j-1, j-1), (j, j+1) \ldots (i-1, i), (i+1, i+1) \ldots$
- 가격표 $j > i$ 가 제거되어 $(1, 1) \ldots (i-1, i-1), (i+1, i) \ldots (j, j-1), (j+1, j+1) \ldots$
와 같다. 이 두 경우를 DP로 처리할 수 있다. 편의상 $j \le i$ 인 경우만 설명하자면, $DP[0][i]$ 를 $a[1 \ldots i], b[1 \ldots i]$ 를 서로 매칭시키는 경우, $DP[1][i]$ 를 $a[1 \ldots i], b[1 \ldots (i+1)]$ 을 서로 매칭시키는 경우의 최솟값으로 정의하자. $DP[0][i]$ 는 prefix max의 형태가 나오고 쉽게 계산할 수 있다. $DP[1][i]$ 의 경우는 두 가지 전이가 가능하다. 하나는 $i, i + 1$ 을 매칭시키고 $DP[1][i-1]$ 을 보는 경우고, 하나는 $i+1$ 을 매칭에서 뺀 후 $DP[0][i-1]$ 을 보는 경우이다. 이 중 최솟값을 취해주면 문제를 해결할 수 있다.
G. Logistical Warehouse 2
인터넷 예선에 나온 Logistical Warehouse와는 조금 내용이 다르다. 가장 큰 차이는 정점 가중치와 간선 가중치가 없다는 점이다. 이것 때문에 문제가 훨씬 쉽게 풀린다고 생각한다.
문제를 조금 다른 형태로 변형해 보자. 트리의 간선을 $k$ 개 지워서, $k + 1$ 개의 연결 컴포넌트로 파티션하는데, 각 연결 컴포넌트에는 정확히 하나의 창고를 지어서 연결 컴포넌트에 있는 정점들을 커버한다고 생각해 보자. 어떠한 연결 컴포넌트를 창고 하나로 커버할 수 있다는 것은, 해당 연결 컴포넌트의 지름이 $2D$ 이하라는 것과 동일하다. 만약 그 이상이면 지름의 양 끝 점 중 하나는 절대 커버할 수 없고, 그렇지 않다면 지름의 중점에 창고를 지으면 된다.
고로, 우리는 트리에서 최소한의 간선을 지워서 모든 연결 컴포넌트의 지름을 $2D$ 이하로 만들고 싶다. 이는 웰노운... 이라고까지는 못 하겠지만 어느 정도 알려진 유형이다. 트리의 지름을 DP로 구하는 것은, 서브트리에서 가장 먼 점과의 거리를 반환하는 DP $farthest[v]$ 를 계산한 후, 어떠한 노드 $v$ 의 자식 $w_1, w_2, \ldots, w_k$ 중 $farthest[w_i] + 1$ 의 합을 최대화하는 두 개를 골라 (두 개가 없으면 하나만 골라) 갱신하는 식으로 할 수 있다.
이 DP를 변형한 그리디 전략을 사용하자. 앞서 말한 식으로 $farthest[v]$ 를 정의하고 Bottom-up으로 해결하는데, 만약 서브트리에서 간선을 지웠다면 $farthest[v]$ 를 계산할 때도 이를 감안한다. 특정 노드에서 문제를 해결할 때, 서브트리의 $farthest[w_i] + 1$ 값을 모은다. 이 중 가장 큰 두 값이 $2D$ 초과이면 간선을 지워줘야 한다. 가장 큰 값부터 순서대로 지워주고, 이하가 되는 순간 바로 반환해 준다.
이 그리디가 정당하다는 사실은 알려져 있다. (엄밀한 증명은 나도 잘 모른다. 다만 직관은 충분한 것 같다.) 시간 복잡도는 $O(N \log N)$ 이다.
그 외에도 아무 정점을 루트로 잡고, 아직까지 다른 창고에 의해 커버되지 않은 가장 깊이가 높은 창고를 반복적으로 선택하는 그리디도 있는데, 이건 $N^2$ 보다 잘 하려면 자료 구조가 필요하다. 관찰을 적당히 하면 세그먼트 트리 선에서 처리 가능한데, 하여튼 위에 적은 그리디 풀이만큼 쉽게 하기는 힘들 것 같다.
H. Postman
본선에서 안 풀린 문제이지만 그만큼 어려운 문제라기 보다는 그냥 노가다가 많다. 노가다가 정말 더럽게 많다. 대회 안이든 밖이든 풀고 싶지는 않은 문제이다.
먼저 $w = 0, w = n$ 인 경우를 따로 처리하자.
- $w = n$ 인 경우는 좌우반전 후 $w = 0$ 인 경우로 볼 수 있다.
- $t = 1$ 인 경우 모든 점이 $x_i > 0$ 을 만족하면 그냥 오른쪽으로 쭉 가면 된다. 아니면 해가 없다.
- $t = 2$ 인 경우 위 조건에 더불어 $x_n = max(x_i)$ 을 만족하면 그냥 오른쪽으로 쭉 가면 된다. 아니면 해가 없다.
이제 $1 \le w \le n - 1$ 임을 가정한다. 일단 $t = 2$ 인 케이스를 풀 수 있으면 $t = 1$ 인 케이스는 모든 끝점을 다 해보면서 풀 수 있다. 물론 그렇게 하면 느리지만, 일단 그 문제는 나중에 생각하고 $t = 2$ 인 케이스부터 먼저 풀어보자.
일반성을 잃지 않고 $x_n > 0$ 이라고 했을 때 (그 외 경우 뒤집음), 방향과 상관 없이 모든 점을 최소 길이로 방문하는 방법은 시작점에서 왼쪽 끝 점을 찍고, 오른쪽 끝 점을 찍고, 그 다음 왼쪽 끝 점을 찍는 것이다. 만약 $x_i < 0$ 인 점과 $x_i > x_n$ 인 점이 모두 존재한다면, 이 방법은 최소 2번의 왼쪽 움직임을 필요로 한다. 이후 이러한 점이 존재함을 가정한다 (없는 3가지 경우는 예외처리 해야 한다. 여기서는 생락한다).
일단 $w = 1$ 인 경우에는 답이 웬만하면 존재하지 않는데, 한 가지 예외가 있다. 만약 $(0, x_n)$ 사이에 점이 없다면, 오른쪽으로 움직인 후 왼쪽 끝으로 점프하고 다시 오른쪽으로 움직이는, 한 바퀴를 약간 더 도는 움직임을 할 수 있다. 아니면 답이 없다. $w \geq 2$ 를 가정하자. 왼쪽 움직임을 두번보다 많이 하면서 하한을 유지하는 방법은, 왼쪽 끝 점을 찍는 과정에서 중간에 있는 점들을 모두 방문하는 것이다. 같은 방식으로 오른쪽 점을 찍고 목적지를 도착할 때도 왼쪽 움직임의 수를 늘릴 수 있다. 이렇게 늘린 후 필요한 왼쪽 움직임 수를 도달했다면 답을 찾았다.
이럼에도 불구하고 답을 못 찾았다면, 이제 $(0, x_n)$ 사이에 있는 점 $i$ 를 방문할 때 $i$ 의 오른쪽의 점을 찍은 후 $i$ 를 방문하는 식으로 왼쪽 움직임을 억지로 늘려줄 수 있다. 이 경우, $i$ 와 $i$ 오른쪽 점의 거리의 2배만큼 손해를 본다. 이를 반복하는 식으로 크기를 늘릴 수 있다. 이는 $(0, x_n)$ 사이에 있는 점들만을 골라서 위치 순으로 정렬한 후, 고른 점의 인접한 거리들을 모아 정렬하는 식으로 계산할 수 있다. 이걸로도 부족하면, 답이 없는 것이다. 이렇게 하면 $t = 2$ 인 경우가 $O(n \log n)$ 에 해결된다.
$t = 1$ 인 경우는 $t = 2$ 인 경우를 $n$ 번 호출하면 되고, 실제 풀이도 대략 그런 방향이지만 이를 약간의 자료 구조로 최적화해야한다. 일반성을 잃지 않고, $x_n > 0$ 인 위치에 도달한다고 생각해 보자. 기본적으로는 왼쪽 끝점을 찍고 오른쪽 끝점을 도달하겠지만, 목적지가 오른쪽 끝점이 아니라면 목적지로 돌아가는 데 추가시간, 그리고 그 사이에 억지로 늘려준 왼쪽 움직임에서 비롯한 추가 시간이 필요할 것이다.
일단 $x_i < 0$ 인 점들은 필요한 왼쪽 움직임의 수를 채워주는 역할만 해주니 개수만 세어 주고 무시하자. 만약 왼쪽 움직임이 찻다면, 왼쪽 끝점을 찍고 오른쪽 끝점에 도달하는 시간이 정답이 된다. 그렇지 않다면 (1) 목적지가 오른쪽 끝점이 아니라면 목적지로 돌아가는 데 추가시간 (2) 그 사이에 억지로 늘려준 왼쪽 움직임에서 비롯한 추가 시간을 벌어와야 한다. 이 두가지에서 번 시간의 합은 남은 왼쪽 움직임의 개수와 동일해야 한다. 오른쪽 끝점의 후보를 위치 순으로 정렬하자 ($0 < x_1 < x_2 < \ldots < x_k$). 오른쪽 끝점 $x_i$ 를 고정시켰을 경우, $x_k - x_i$ 만큼의 추가시간이 들며, $(k - i)$ 개의 왼쪽 움직임을 벌어온 것이다. 만약에 여전히 왼쪽 움직임이 부족하다면, 그 사이에 있는 인접한 거리들 중 작은 것을 골라서 움직임을 더 채워줘야 한다.
$x_k, x_{k - 1}, \ldots$ 와 같이 좌표가 감소하는 순으로 보았다면, 이는 원소가 삭제되는 집합에서 가장 작은 $k$ 개의 원소를 찾는 문제와 동일하다. 다만, 원소가 하나 삭제되면, 쿼리로 물어보는 숫자 $k$ 도 하나씩 줄어든다는 점에 유의해야 한다. 이는 std::set 을 사용하여 해결할 수 있다. 현재 가장 작은 $k$ 개의 원소와 그 합을 관리한 후, 이번 턴에 삭제해야 하는 원소가 집합에 있으면 집합에서 그 원소를 지우고, 아니면 가장 큰 원소를 지운다. 이렇게 하면 집합에 들어있는 원소는 쿼리에서 물어보는 $k$ 개의 원소에 정확히 대응된다.
여담으로 $t = 1$ 인 경우에 $w = n - 1$ 이면 숫자가 잘 안 맞아서 아마 예외처리 해야 할 것이다. 적어도 난 그렇게 했다.
최종 시간 복잡도는 $O(n \log n)$ 이다.
I. Security System
논문 Guarding monotone art galleries with sliding cameras in linear time 에서 다루는 문제와 동일하다. 여기서도 논문에 나온 풀이를 설명한다.
먼저 $x$-단조 다각형을 연속된 사각형의 형태로 쪼개주자. 세로 선분을 발견할 때마다 해당 세로 선분을 기준으로 다각형을 쪼개주면, 다각형 전체가 $x = c$ 라는 직선들에 의해 여러 개의 사각형으로 쪼개진다. $x$-단조 다각형이니, 같은 $x$ 좌표 구간에 두 개 이상의 다각형이 있지 않다. 더해, 이 문제에서 가로 선분의 실질적인 길이는 중요하지 않으니, 결국 각 사각형에 대해서 중요한 것은 이 사각형의 $y$ 좌표 구간 뿐이다. 결론적으로 주어진 도형을 $n/2$ 개 정도의 구간이 붙어있는 것으로 생각할 수 있다. 각 구간을 $V_1, V_2, \ldots, V_k$ 라고 정의하자.
앞에서부터 가로 로봇과 세로 로봇을 채워나가는 식으로 문제를 해결할 것이다. 정확히는, 동적 계획법을 사용한다. 다음과 같이 상태를 정의한다.
- $A[i] = V_{i + 1} \ldots V_k$ 를 덮는 데 필요한 최소 개수의 로봇
- $B[i] = $ $V_i$ 의 오른쪽 끝에 세로 로봇이 있어서 $V_{i + 1} \ldots V_k$ 의 일부 왼쪽 영역이 덮여있다고 가정했을 때 $V_{i + 1} \ldots V_k$ 를 덮는 데 필요한 최소 개수의 로봇
즉, $A[i]$ 는 마지막에 가로 로봇을 둔 경우를 표현하고, $B[i]$ 는 마지막에 세로 로봇을 둔 경우를 표현한다.
이제 상태 전이를 관찰한다. 먼저 $A[i]$ 부터 보자.
- 가로 로봇 오른쪽에 가로 로봇이 붙는다면 둘은 독립이다. $i_1$ 을 $V_{i+1} \ldots V_{i_1}$ 이 하나의 가로 로봇으로 덮이는 가장 큰 $i_1$ 이라고 하면, $A[i] \le A[i_1] + 1$ 이다.
- 가로 로봇 $x$ 오른쪽에 세로 로봇 $y$ 가 붙는다면, $x$ 와 $y$ 사이에 덮이지 않는 영역이 생기지 않는 한 $y$ 를 최대한 오른쪽에 배치할 수 있다. $i_2$ 를 $V_{i+1} \ldots V_{i_2}$ 가 $V_{i_2}$ 오른쪽에 붙어 있는 세로 로봇으로 모두 덮어지는 가장 큰 $i_2$ 라고 정의하자. $A[i] \le B[i_2] + 1$ 이다.
$B[i]$ 도 비슷하다.
- 세로 로봇 $x$ 오른쪽에 가로 로봇 $y$ 가 붙는 경우, $x$ 와 $y$ 사이에 덮이지 않는 영역이 생기지 않는 한 $y$ 를 최대한 오른쪽에 배치할 수 있다. $i_1$ 을 $V_{i+1} \ldots V_{i_1}$ 이 $V_{i}$ 오른쪽에 붙어 있는 세로 로봇으로 모두 덮어지는 가장 큰 $i_1$ 이라고 정의하자. 그리고 $i^\prime_1$ 을 $V_{i_1 + 1} \ldots V_{i^\prime_1}$ 이 하나의 가로 로봇으로 덮이는 가장 큰 $i^\prime_1$ 이라고 하면, $B[i] \le A[i^\prime_1] + 1$ 이다.
- 세로 로봇 $x$ 오른쪽에 세로 로봇 $y$ 가 붙는 경우, $x$ 와 $y$ 사이에 덮이지 않는 영역이 생기지 않는 한 $y$ 를 최대한 오른쪽에 배치할 수 있다. $i_2$ 를 $V_{i+1} \ldots V_{i_2}$ 가 $V_{i}$ 오른쪽에 붙어 있는 세로 로봇과 $V_{i_2}$ 오른쪽에 붙어 있는 세로 로봇으로 모두 덮어지는 가장 큰 $i_2$ 라고 정의하자. $B[i] \le B[i_2] + 1$ 이다.
이렇게 정의를 할 경우 문제에서 요구하는 겹치지 않음 등의 조건은 자동적으로 만족된다. DP의 엄밀한 증명은 이런 저런 가정들이 필요한데, 그 내용이 정말 길다. 관심이 있다면 링크된 논문을 참고하면 좋을 것 같다.
이제 각 $i$ 에 대해서 필요한 인덱스들을 적당히 구할 수 있다면, 전체 문제는 $O(n)$ 에 쉽게 해결된다. 중요한 것은 저 인덱스들을 어떻게 효율적으로 구하느냐인데, 각각 대략 다음과 같이 할 수 있다.
- 모든 $i$ 에 대해서, $V_{i + 1} \ldots V_j$ 의 교집합의 길이가 1 이상인 최대 $j$ 를 $O(n \log n)$ 에 구할 수 있다. 다양한 방법이 있고 그 중에는 $O(n)$ 에 되는 방법도 있는데, 내가 생각하는 가장 깔끔한 방법은 이것인 것 같다. $V_{i + 1} \ldots V_j$ 의 교집합의 길이가 0임은, 그 사이에 교집합의 길이가 0인 구간 쌍이 존재한다는 것이다. $Collision[i]$ 를 $V_i= (s_i, e_i), V_j = (s_j, e_j)$ 가 겹치지 않는 최소 $j$ 라고 하자. 식으로는, $e_i \le s_j$ 혹은 $e_j \le s_i$ 를 만족하는 최소 $j$ 이다. 이는 $s_j$ 에 대한 단조적인 Stack을 관리하면 이분 탐색으로 각각 $O(\log n)$ 에 구할 수 있고, 이제 최대 $j$ 는 $Collision[i]$ 의 suffix min 형태로 표현할 수 있다. 하여튼 이렇게 해서 $A[i]$ 의 $i_1$, $B[i]$ 의 $i_1 \rightarrow i^\prime_1$ 을 해결할 수 있다.
- $A[i]$ 의 $i_2$ 는 특정 위치 $i$ 에서 $V_{i+1} \subseteq V_{i+2} \subseteq \ldots \subseteq V_j$ 를 만족하는 최대 $j$ 이다. $O(n)$ 에 구할 수 있다.
- $B[i]$ 의 $i_1$ 은 특정 위치 $i$ 에서 $V_{j} \subseteq V_{j-1} \subseteq \ldots \subseteq V_{i+1}$ 를 만족하는 최대 $j$ 이다. $O(n)$ 에 구할 수 있다.
- $B[i]$ 의 $i_2$ 는 다음과 같은 관찰이 필요한데, $V_{i+1} \ldots V_{i_2}$ 구간의 교집합이 비지 않아야 하며, 시작점이 증가하다가 감소하는 Bitonic, 끝점이 감소하다가 증가하는 Bitonic 형태여야 한다. (여기서 교집합이 비지 않는다는 게 위에서 정의한거랑 다르다 . 위에서는 개구간을 쓰고 여기서는 폐구간을 쓴다. 즉 위에서는 $(1, 5) (5, 9)$ 는 교집합이 없지만 여기서는 $(1, 5), (5, 9)$ 는 교집합이 있다. $e_i < s_j, e_j < s_i$ 를 만족해야 안 겹친다는 뜻이다.) 그래서 해당 세 가지 조건을 만족하는 최대 길이 구간을 구해야 한다. 맨 첫번째 조건은 위에서 적은 것과 비슷하게 하면 되고, 두 세번째 조건은 DP로 하면 된다. $O(n \log n)$ 에 구할 수 있다.
여담으로 이게 로봇이 벽에 끝점 말고는 닿을 수 없어서 참 고달픈데... 알아서 잘 해보자. 시간 복잡도는 $O(n \log n)$ 이다.
J. Squid Game
이 글 에 보면 예전 수학 올림피아드에 이 문제가 나왔던 예시들이 몇 가지 서술되어 있다. 본인은 이 문제에 대해 큰 직관은 없고, 여기 있는 내용 과 위 글에 있는 내용 기반으로 정리한다.
$q = \lfloor \frac{Y}{X} \rfloor$ 라고 정의하고, 두 가지 케이스로 나누자.
- $Y \pmod X \le X / 2$ 인 경우: $q$ 를 이진수로 나타내면 $q = \sum_{i} 2^i b_i$ ($b_k b_{k - 1} \ldots b_0 (2)$) 와 같이 쓸 수 있다. 이제, 모든 $i = 0, 1, \ldots, k$ 에 대해서, 만약 $b_i = 1$ 이면 $X \leftarrow Y$ 로 붓고, 아니면 $X \leftarrow Z$ 로 붓는다. 이 때, $Y$ 에서 부은 양은 $Z$ 에서 부은 양보다 항상 많기 때문에 (최소 $2^k X$ 이니), 이 작업을 하다가 $Z$ 에서 물이 동날 가능성은 없다. 결론적으로 $Y := Y \pmod X$ 가 되고, 물의 양을 최소화하는 위치 역시 $Y$ 가 된다. 이 때 $Y \le X/2$ 가 만족된다. 고로 이 과정을 거치면 최솟값의 크기가 반 이하로 줄어든다.
- $Y \pmod X > X / 2$ 인 경우: $q+1$ 을 이진수로 나타내면 $q+1 =\sum_{i} 2^i b_i$ ($b_k b_{k - 1} \ldots b_0 (2)$) 와 같이 쓸 수 있다. 이제, 모든 $i = 0, 1, \ldots, k-1$ 에 대해서, 만약 $b_i = 1$ 이면 $X \leftarrow Y$ 로 붓고, 아니면 $X \leftarrow Z$ 로 붓는다. $Z$ 에서 부은 양이 $Y$ 의 전체 물양보다 항상 적기 때문에, 이 작업을 하다가 $Z$ 에서 물이 동날 가능성은 없다. 이제 $i = k$ 인 경우는 다음과 같이 처리한다. 현재 $(X^\prime, Y^\prime) = (2^k X, Y - (q+ 1- 2^k)X)$ 이다. 여기서 $Y^\prime$ 을 2배 하고, $X$ 에서 물을 퍼 온다. 이 경우 $X$ 의 물 양은 $2^k X - Y + (q+ 1 - 2^k) X = (q+ 1)X - Y = X - Y \pmod X$ 가 된다. 고로 이 과정을 거치면 최솟값의 크기가 반 이하로 줄어든다.
이 과정은 최대 $\log (10^9)$ 번 반복된다. 그리고 $q$ 의 길이도 $\log (10^9)$ 이다. 고로 $\log^2 (10^9)$ 번의 연산 안에 문제를 해결할 수 있다.
여담으로 두 번째 케이스를 구현 안 하고 첫 번째 케이스만 구현할 경우에는 유한 시간 안에 끝나기는 하지만 $\log^2 (10^9)$ 번 안에 끝남은 보장되지 않는다. 고로 틀린 풀이라고 봐야겠으나, 반례는 잘 모르겠고, 대회 데이터에서는 두 번째 케이스를 구현 안 해도 AC가 잘 나온다.
K. Stock Price Prediction
CEOI 2011 기출이다. 서강대에도 비슷한 문제가 있다. 사실 이 정도는 우연이라고 생각할 수 있지만, 이후 SCPC 등에서 비슷한 문제가 과하게 많이 나와서, 결국 유형을 복습했는가 안 했는가를 기준으로 솔브가 갈리지 않았나 싶다.
풀이에 대해서도 이미 잘 설명된 인터넷 자료가 있으니 길게 설명하지는 않겠다. 간단하게 요약하면 KMP의 원리를 사용한다. 두 문자열이 매칭된다는 것을, 두 문자열의 좌표압축 값이 같다는 것으로 정의하자. 이 정의를 사용하여 Failure function을 구하는데, 현재 Failure function에서 처리하고 있는 Suffix를 이루는 문자들을 Fenwick tree등에 관리하자. 이렇게 되면 새로운 문자가 들어왔을 때 이 문자가 좌표압축 이후 어떠한 값을 가지고 있는지를 계산할 수 있다. 원래 문자열에 대해, $S[1 \ldots i]$ 에서 $a[i]$ 의 좌표압축된 값을 계산해 두면, 이 값이 문자열과 매칭하는지 역시 알 수 있다. 이제 Failure function을 구하였다면, 문자열의 매칭을 구하는 것은 Failure function을 구하는 것과 유사하게 하면 되다.
Fenwick tree 안 쓰고 선형 시간에도 할 수 있는데, 쓰는 쪽이 더 생각하기 간단하다.
조금 더 자세한 설명을 구한다면 다음과 같은 자료들이 참고가 될 것이다.
- https://oi.edu.pl/static/attachment/20110713/ceoi-2011.pdf (15p - 18p)
- https://acm.sogang.ac.kr/spc/contest/2020/solutions.pdf (H. 파인애플 피자)
L. Trio
가능한 답의 후보 $(i, j, k)$ ($i < j < k$) 를 모두 열거하자. 두 개의 수 $A[j], A[k]$를 고정했을 경우, 두 수의 자릿수에 따라 세 번째로 골라야 하는 수의 형태가 정해진다.
- 만약 어떠한 자릿수에서 두 수가 같다면, 세 번째 수 역시 같은 수를 따라야 한다.
- 다르다면, 세 번째 수 역시 두 수와 달라야 한다.이러한 조건을 만족하는 수가 $A[1], A[2], \ldots, A[j - 1]$ 중 몇 개인지 알아야 한다.
해당 형태의 수를 직접 나열하게 되면 $8^4$ 개의 가짓수가 있으니 Naive 풀이에 비해 크게 좋지 않다. 포함 배제를 사용하자. $11 \times 11 \times 11 \times 11$ 크기의 배열 $cnt$ 를 만들고, 숫자 $abcd$ 가 존재하면 $cnt[a][b][c][d]$ 를 1 늘려주자. 이 때, 배열의 각 차원의 크기가 10이 아니라 11인데, 만약 어떤 자릿수의 인덱스가 10일 경우 이 자리에는 모든 수가 들어올 수 있다는 것을 뜻한다. 예를 들어, $cnt[1][10][10][7]$ 은 1**7 형태의 수, 즉 1007, 1017, ..., 1997 이라는 수들의 등장 횟수 합이다.
만약, $A[1], A[2], \ldots, A[j - 1]$ 에 대해서 위 카운트를 저장해 놓은 배열이 있다면 다음과 같은 규칙으로 자릿수를 하나씩 맞춰가면서 백트래킹을 할 수 있다.
- 만약 어떠한 자릿수에서 두 수가 같다면, 세 번째 수의 해당 자릿수는 고정이다. 고로 바로 다음 자릿수로 넘어간다.
- 다르다면, 전체 경우 (10) 를 계산하고 두 경우를 빼어 준다.
각 백트래킹 상태에서 최대 3개의 브랜치가 생성되니 $3^4$ 시간에 합을 계산할 수 있다. $A[1], A[2], \ldots, A[j - 1]$ 에서 $A[j]$ 를 추가하는 것은, 그냥 각 자릿수에 대해서 원래 수를 유지할 지 10을 적을 지를 $2^4$ 의 경우의 수로 다 해보면 된다. 종합하면 시간 복잡도 $O(3^4 \times N^2)$ 에 문제가 해결된다.
'공부 > Problem solving' 카테고리의 다른 글
| Push Relabel Algorithm (1) (0) | 2022.02.15 |
|---|---|
| 2021.12.02 problem solving (0) | 2021.12.02 |
| 2021 ICPC 서울 인터넷 예선 (4) | 2021.10.13 |
| APIO 2021 (1) | 2021.07.29 |
| Klein's Algorithm for Computing Edit Distance on Tree (0) | 2021.07.27 |
- Total
- Today
- Yesterday
