티스토리 뷰
https://www.acmicpc.net/problem/12010
이해가 안가면 이 글과 참고해서 보면 좋다 : http://usaco.org/current/data/sol_landscape_platinum_open16.html
여담으로 이 문제는 KOI 2005 소방차와 상당히 유사한 문제다. 같이 보면 좋을 듯 하다. http://koistudy.net/?mid=prob_page&NO=313
1. O((NK)^2)
dirt의 개수만큼 위치를 저장해 놓은 수열을 펴보자. 예를 들어 3, 1, 5, 1과 같이 수열이 주어지면 0, 0, 0, 1, 2, 2, 2, 2, 2, 3과 같은 형태로 수열을 바꾸는 것이다.
수열 A, B가 있을 때 진행하는 연산에 대해서 다시 생각해 보면
* 1. 추가 -> 수열 B에 있는 값 하나를 cost X로 추가
* 2. 제거 -> 수열 A에 있는 값 하나를 cost Y로 제거
* 3. 편집 -> 수열 A에 있는 값 하나와, B에 있는 값 하나를 찾아서, cost Z * |Ai - Bj|로 변환
edit distance 같아 보이고 실제로 그렇게 되지만, 자명하지 않다. 일단 지금까지 확실히 알아낸 건 A와 B에 있는 두 수를 매칭시키면서 최소 비용을 찾는 알고리즘이라는 것이다. (고로.. min cost max flow로도 풀 수 있다.)
이제 매칭이 교차하지 않는다는, 즉 임의의 매칭 (i1, j1) / (i2, j2)에 대해서 (i1 < i2 && j1 < j2) 혹은 (i2 < i1 && j2 < j1) 이라는 사실을 증명해야 한다. 이는 교차하는 매칭을 항상 그렇지 않게 swapping 해주어서 똑같은 비용의 비교차 매칭으로 바꿀 수 있음을 보임으로써 증명 가능하다.
여기까지 오면 소방차 (Small) 문제와 똑같다는 것을 알 수 있다. http://koistudy.net/?mid=prob_page&NO=721 이제 흔한 DP로 O((NK)^2)에 풀 수 있다.
2. O(NK)
DP는 잊고, 다시 매칭으로 돌아가자. 문제를 정리해보면
* 기본적으로 X * m + Y * n의 cost를 소모한다.
* 편집 쌍을 하나 만들어주면, (X + Y - |Aj - Bj| * Z) 만큼의 비용을 절감할 수 있다.
* 최소의 비용을 만들어야 한다.
A와 B의 수열의 위치를 수직선에 쫘라락 늘어놓자. 몇가지 관찰들의 연속으로 문제를 해결할 수 있다.
첫번째 관찰은, 수직선의 (l1, r1) 매칭 쌍과 (l2, r2) 매칭 쌍이 존재하고, 이 둘이 겹친다면, (l1 <= l2 <= r2 <= r1 || l2 <= l1 <= r1 <= r2) 의 형태로 매칭 쌍을 변형할 수 있다는 것이다. 즉, 매칭 쌍은 disjoint or nested의 관계이다.
두번째 관찰은, 하나의 매칭 쌍이 있을 때, 이 매칭 쌍 안에 포함되는 모든 수들은 매칭을 이룬다는 것이다. 즉, (l1, r1) 매칭 쌍이 있을 때, (l1 < x < r1)을 만족하는 모든 x들은 자기들끼리 매칭이 있어야 한다. 이유는, 그 안에 매칭을 못 이룬 빈 수가 있으면, 그 수를 잇는 매칭 쌍으로 변형해서 비용을 더욱 더 절감할 수 있기 때문이다. (여기서는 x 좌표가 같은 점에 대해서 언급하지 않았지만, 그 부분은 알아서 잘 해결하면 된다... 뭐라 설명해야 하지)
세번째 관찰은, 하나의 매칭 쌍이 있을 때, 그 매칭 쌍 안에 있는 A의 개수와 B의 개수는 같다는 것이다. 이유는 두번째와 똑같다. 세번째 관찰을 통해서 우리는 A와 B를 분류할 수 있는데,
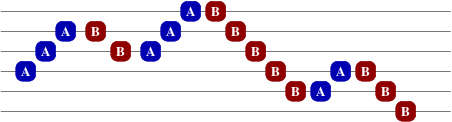
괄호 문자열과 상당히 비슷한 방법으로 A와 B를 나열가능하고, 같은 floor끼리의 매칭만 고려하면 된다.
같은 floor끼리의 매칭만 고려하는 조건이 왜 유용할까? 같은 floor라는 것은, 연속된 A와 B가 그 floor에 존재하지 않는다는 것을 의미한다. 이는 상당히 유용한 조건을 만들어낸다. 먼저, 완벽 매칭에 대해서만 생각을 해보자 - 즉 모든 수가 매칭에 포함되어야 한다는 조건이 있을 때에 대한 생각이다. 이 때는 |A| = |B|일 것이고, A와 B를 그냥 정렬해서 작은 애들끼리 ~ 큰 애들 끼리 순서대로 묶어주면 됨을 쉽게 증명할 수 있다.
이제, DP[x] = [0, x]까지의 수가 매칭되었을 때의 min cost라고 생각해보면
* Case 1 : x가 매칭에 없다 -> 자명히 DP[x-1]
* Case 2 : x가 y와 매칭한다 -> [y+1, x-1]의 매칭의 결과는 정해진다. 이를 계산해두고, DP[y-1]의 값과 결합
DP[n-1] 에 대해서 생각해보면, 재귀적으로 잘 정의되며, 이렇게 DP를 구할 수 있다. Naive는 O(N^3)이지만, O(N)으로 줄일 수 있고, 나머지 루틴 역시 카운팅 정렬등을 동반하면 O(NK)에 쉽게 풀림을 알 수 있다.
여담으로 min cost flow 등으로도 풀린다고 한다 (APIO 2007 backup과 유사한 아이디어일 것이다.) 난 잘 모르겠으니 아는 분 있다면 댓글로 알려주시면 감사.
( + CF에 simple greedy 풀이가 있다. 읽어봤는데 상당히 신기함. 아주 깔끔하게 생각하셨다. 왜 되는지 잘은 모르겠지만 틀린거 같지는 않다. http://codeforces.com/blog/entry/44054?#comment-288014 참고.)
'공부 > Problem solving' 카테고리의 다른 글
| 각도 정렬하기 (7) | 2016.05.21 |
|---|---|
| CEOI 2006 (0) | 2016.05.17 |
| Harbingers (CEOI 2009) (4) | 2016.04.28 |
| 2016.04.19 problem solving (0) | 2016.04.19 |
| 1일 1DP 2016.04.06 solution (1) | 2016.04.09 |
- Total
- Today
- Yesterday
